设F(x)是连续型随机变量的分布函数．证明对任意a＜b 有 ∫—∞+∞[F(x+b)一F(x+a)]

大学本科已帮助：人时间:2023-11-14 05:02:04

设F(x)是连续型随机变量的分布函数．证明对任意a＜b，有 ∫—∞+∞[F(x+b)一F(x+a)]dx=b一a．
请帮忙给出正确答案和分析，谢谢！

470***444

2023-11-14 05:02:04



正确答案：设X的概率密度为f(x)则有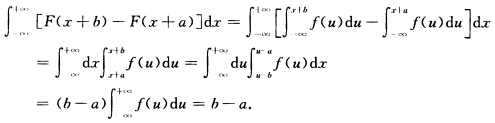
将F(x+a)，F(x+6)用X的概率密度f(x)表示，然后交换积分顺序，并注意此时内层积分与积分变量无关，最后用到∫—∞+∞f(x)dx=1．

设随机变量X的概率密度为求一可导单调增加函数g(x)．使得Y=g(X)服从参数为λ的指数分布．请

设随机变量X的概率密度为求一可导单调增加函数g(x)．使得Y=g(X)服从参数为λ的指数分布．请帮忙给出正确答案和分析，谢谢！
设在时间t(分钟)内通过某交叉路口的汽车数服从参数与f成正比的泊松分布．已知在一分钟内没有汽车通过

设在时间t(分钟)内，通过某交叉路口的汽车数服从参数与f成正比的泊松分布．已知在一分钟内没有汽车通过的概率为0．2，求在2分钟内有多于1辆汽车通过的概
设A1 A2 A3为三个随机事件下列等式不正确的是( )．A．A1(A2一A3)=(A1A2)—(

设A1，A2，A3为三个随机事件，下列等式不正确的是( )．A．A1(A2一A3)=(A1A2)—(A1A3)B．A1∪A2=A1A2∪(A1一A2)∪(A2一A1)C．D．请帮忙给出正确答案和分析，谢谢！
设随机变量X的分布函数则P{X=1)=( )．A．0B．C．D．e—1请帮忙给出正确答案和分析谢

设随机变量X的分布函数，则P{X=1)=( )．A．0B．C．D．e—1请帮忙给出正确答案和分析，谢谢！
设随机变量X的分布函数为求：①常数A； ②P{0．2＜X＜1．2)； ③X的概率密度．请帮忙给出

设随机变量X的分布函数为求：①常数A； ②P{0．2＜X＜1．2)； ③X的概率密度．请帮忙给出正确答案和分析，谢谢！

设随机变量X的概率密度为求一可导单调增加函数g(x)．使得Y=g(X)服从参数为λ的指数分布．请