设函数f(x)在[0 1]上可微 对于[0 1]上每一个x 函数f(x)的值都在开区间(0 1)内

正确答案：令F(x)＝f(x)－x由题设可知F(x)在[01上连续又因0＜f(x)＜1所以 F(0)＝f(0)－0＞0F(1)＝f(1)－1＜0 由闭区间上连续函数的零点定理可知在(01)内至少有一个x使F(x)＝0即f(x)＝x． 用反证法证F(x)在(01)内至多有一个零点． 若不然x₁x2∈(01)x₁＜x₂使得 f(x₁)＝x₁f(x₂)＝x₂ 由拉格朗日中值定理至少存在一个x∈(x₁x)∈(01)使得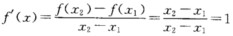与题设矛盾．综上所述命题得证．
令F(x)＝f(x)－x,由题设可知F(x)在[0,1上连续,又因0＜f(x)＜1,所以F(0)＝f(0)－0＞0,F(1)＝f(1)－1＜0由闭区间上连续函数的零点定理可知,在(0,1)内至少有一个x,使F(x)＝0,即f(x)＝x．用反证法证F(x)在(0,1)内至多有一个零点．若不然,x1,x2∈(0,1),x1＜x2,使得f(x1)＝x1,f(x2)＝x2由拉格朗日中值定理,至少存在一个x∈(x1,x)∈(0,1),使得与题设矛盾．综上所述,命题得证．