一颗质量为m的炮弹 以速率v飞行．其内部炸药爆炸使此炮弹分裂为两块弹片．爆炸后 弹片增加的动能为T
一颗质量为m的炮弹，以速率v飞行．其内部炸药爆炸使此炮弹分裂为两块弹片．爆炸后，弹片增加的动能为T，且一块的质量为另一块质量的k倍(k＞1)．如二者仍沿原方向飞行，试证其速率分别为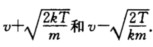
请帮忙给出正确答案和分析，谢谢！
参考解答
463***100
2024-11-04 00:56:37
正确答案：设一块弹片质量为m1则另一块弹片质量为m2已知m1=km2且m1+m2=m于是有
又设m1的速度为v1m2的速度为v2则弹片增加的动能可以表示为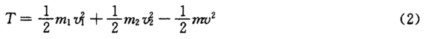
因为爆炸过程中内力很大故外力可以忽略动量守恒．因此 mv=m1v1+m2v2 (3)联立式(1)和(3)解得 v2=(k+1)v—kv1 (4)将式(4)代入式(2)解得
将其代入式(4)有
已知炮弹爆炸成两弹片后仍沿原方向飞行故只能取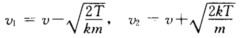
设一块弹片质量为m1,则另一块弹片质量为m2,已知m1=km2且m1+m2=m于是有又设m1的速度为v1,m2的速度为v2,则弹片增加的动能可以表示为因为爆炸过程中内力很大,故外力可以忽略,动量守恒．因此mv=m1v1+m2v2(3)联立式(1)和(3),解得v2=(k+1)v—kv1(4)将式(4)代入式(2),解得将其代入式(4),有已知炮弹爆炸成两弹片后仍沿原方向飞行,故只能取
相似问题
用绳系一个小物块使之在光滑水平面上作圆周运动 圆半径为r0 速率为v0．今缓慢的拉下绳的另一端 使圆
用绳系一个小物块使之在光滑水平面上作圆周运动，圆半径为r0，速率为v0．今缓慢的拉下绳的另一端，使圆半径逐渐减小．求圆半径缩短至r时，小物块的速率为
振动和波动有什么区别与联系? 简谐振动方程和简谐波动方程有什么区别与联系? 振动曲线和波形曲线又有什
振动和波动有什么区别与联系? 简谐振动方程和简谐波动方程有什么区别与联系? 振动曲线和波形曲线又有什么不同?请帮忙给出正确答案和分析，谢谢！
一个质量为1kg的物体 置于水平地面上 物体与地面之间的静摩擦系数为μ0=0．20 滑动摩擦系数为μ
一个质量为1kg的物体，置于水平地面上，物体与地面之间的静摩擦系数为μ0=0．20，滑动摩擦系数为μk=0．16，现对物体施加一个水平拉力F=t+0．96(SI)，则2
一列平面简谐机械波在介质中传播时 若一个介质元在时刻t的机械能是10J 则在时刻(t+T)(T为波的
一列平面简谐机械波在介质中传播时，若一个介质元在时刻t的机械能是10J，则在时刻(t+T)(T为波的周期)该介质元的振动动能是_________．请帮忙给出正确答案
求地球和月球的质心位置。已知地球 月球质量分别为 M = 5.98× 1024 kg 和 m = 7
求地球和月球的质心位置。已知地球、月球质量分别为 M = 5 98× 1024 kg 和 m = 7 35× 1022 kg ，地球中心与月球中心的距离为 L = 3 84
