证明：对于实数域上任一s×n矩阵A 都有rank(AATA)=rank(A)．请帮忙给出正确答案和分

正确答案：设η为Ax=0的解则Aη=0AA^TAη=AA^T0=0所以η亦为AA^TAx=0的解．设叩为AA^TAx=0的解则AA^TAη=0A^TAA^TAη=0．从而ηA^TAA^TAη=0即(A^TAη)^TA^TAη=0设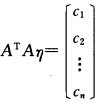．则c_n²+c_n²+…+c_n²=0因为c₁c₂…c_n为实数所以c₁=c₂一…c_n=0．故A^TAη=0η^TA^TAη=0．即(Aη)^TAη=0令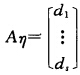则d₁²+d₂²+…+d_s²=0因为d₁d₂…d_s为实数所以d₁=d₂=…=d_s=0．所以η为Ax=0的解．综上所述AA^TAx=0与Ax=0同解．所以n一rank(AA^TA)=n-rank(A)因此有rank(AA^TA)=rank(A)．
设η为Ax=0的解,则Aη=0,AATAη=AAT0=0,所以η亦为AATAx=0的解．设叩为AATAx=0的解,则AATAη=0,ATAATAη=0．从而ηATAATAη=0,即(ATAη)TATAη=0,设．则cn2+cn2+…+cn2=0,因为c1,c2,…,cn为实数,所以c1=c2一…cn=0．故ATAη=0,ηTATAη=0．即(Aη)TAη=0令则d12+d22+…+ds2=0,因为d1,d2,…,ds为实数,所以d1=d2=…=ds=0．所以η为Ax=0的解．综上所述,AATAx=0与Ax=0同解．所以n一rank(AATA)=n-rank(A),因此有rank(AATA)=rank(A)．