设y1 y2是一阶线性非齐次微分方程y＋p(x)y＝q(x)的两个特解．若常数λ μ使λy1＋μy2
设y1，y2是一阶线性非齐次微分方程y＋p(x)y＝q(x)的两个特解．若常数λ，μ使λy1＋μy2是该方程的解，λy1－μy2是对应的齐次方程的解，则
A．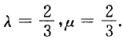
B．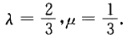
C．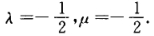
D．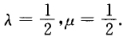
请帮忙给出正确答案和分析，谢谢！
参考解答
463***101
2024-11-09 11:28:46
正确答案：A
[分析此题主要考查线性微分方程解的性质和结构．[详解因λy1－μy12是方程y'＋p(x)y＝0的解，所以(λy1－μy2)'＋p(x)(λy1－μy2)＝0，即λ[y'1＋p(x)y1－μ[y'2＋p(x)y2＝0．由已知得(λ－μ)q(x)＝0，因为q(x)≠0，所以λ－μ＝0，又λy1＋μy21是非齐次方程y'＋p(x)y＝q(x)的解，故(λy1＋μy2)'＋p(x)(λy1＋μy2)＝g(x)．即λ[y'1＋p(x)y1－μ[y'2＋p(x)y2＝q(x)．由已知得(λ＋μ)q(x)＝g(x)．因为q(x)≠0，所以λ＋u＝1，解得[评注此题属反问题，题目构造较新颖．
相似问题
求下列微分方程的通解: (1)yˊ＋y＝e－x； (2)yˊ＋2xy＝4x； (3)xyˊ＝x－y；
求下列微分方程的通解: (1)yˊ＋y＝e－x； (2)yˊ＋2xy＝4x； (3)xyˊ＝x－y； (4)(x2＋1)yˊ＋2xy＝4x2； (5)xyˊ＋y＝xex； (6)yˊ＋ytanx＝cosx
求下列曲线所围成的图形的面积： 请帮忙给出正确答案和分析 谢谢！
求下列曲线所围成的图形的面积： 请帮忙给出正确答案和分析，谢谢！
微分方程(y＋x2)dx－2xdy＝0满足的特解为______．请帮忙给出正确答案和分析 谢谢！
微分方程(y＋x2)dx－2xdy＝0满足的特解为______．请帮忙给出正确答案和分析，谢谢！
求下列曲线所围成的图形的面积： (1)ρ＝asin3φ； (2)ρ2＝a2cos2φ．请帮忙给出正确
求下列曲线所围成的图形的面积： (1)ρ＝asin3φ； (2)ρ2＝a2cos2φ．请帮忙给出正确答案和分析，谢谢！
下列各题中哪些函数是同一函数的原函数： (1)1／2sin22x －1／4cos2x －1／4c
下列各题中哪些函数是同一函数的原函数： (1)1／2sin22x， －1／4cos2x， －1／4cos2x； (2)1nx， ln2x， ln ｜x｜， 1nx＋C请帮忙给出正确答案和分析，谢谢！
