在半径为a的球面上 电势分布为f(θ) 试求在球内 外区域中的电势分布。请帮忙给出正确答案和分析 谢

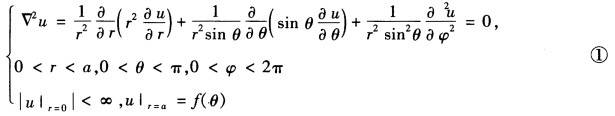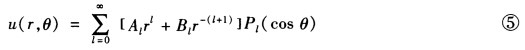正确答案：(1)球内电势的定解问题为因为问题具有轴对称性u应与φ无关故可令u=u(rθ)=Θ代入问题①中的方程有方程④是Legendre方程加上自然条件|Θ(±1)|＜+∞得式④的本征值ι=n(整数)和本征函数Θ(x)=C_nP_n(x)于是得问题一般解为用边界条件可决定待定系数A_ιB_ι。由u在极点有界的边界条件知B_ι=0故球内问题的解为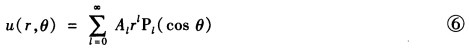由球面上的边界条件可得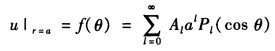这时需将函数f(θ)按P_ιcos θ)的广义Fourier级数展开。按公式应有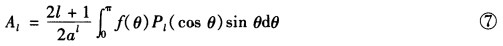代入式⑥既得球内电势分布为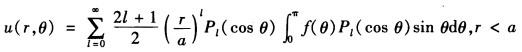(2)球外电势的定解问题为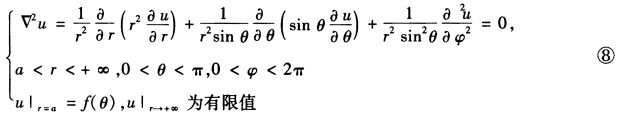问题依然具有轴对称性故一般解仍为式⑤。由无穷远处的条件知A_ι=0所以球外解为将式⑨代入到球面的边界条件中可得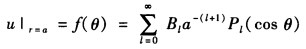其展开式系数为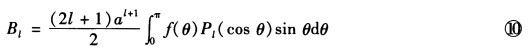将式⑩代入式⑨即得球外电势分布为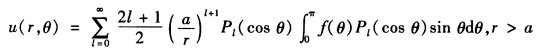
(1)球内电势的定解问题为因为问题具有轴对称性,u应与φ无关,故可令u=u(r,θ)=Θ,代入问题①中的方程有方程④是Legendre方程,加上自然条件|Θ(±1)|＜+∞得式④的本征值ι=n(整数)和本征函数Θ(x)=CnPn(x)于是得问题一般解为用边界条件可决定待定系数Aι,Bι。由u在极点有界的边界条件知,Bι=0,故球内问题的解为由球面上的边界条件,可得这时需将函数f(θ)按Pιcosθ)的广义Fourier级数展开。按公式应有代入式⑥,既得球内电势分布为(2)球外电势的定解问题为问题依然具有轴对称性,故一般解仍为式⑤。由无穷远处的条件知,Aι=0,所以球外解为将式⑨代入到球面的边界条件中,可得其展开式系数为将式⑩代入式⑨,即得球外电势分布为