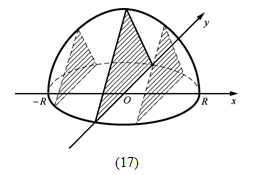
计算底面是半径为R的圆 而垂直于底面一固定直径的所有截面都是等边三角形的立体体积.见图17.
计算底面是半径为R的圆，而垂直于底面一固定直径的所有截面都是等边三角形的立体体积.见图17.
参考解答
463***114
2025-02-05 06:18:47
解：以底面上的固定直径所在直线为x轴，过该直径的中点且垂直于x轴的直线为y轴，建立平面直角坐标系，则底面圆周的方程为：x2+y2=R2．
过区间[-R，R上任意一点x，且垂直于x轴的平面截立体的截面为一等边三角形，若设与x对应的圆周上的点为(x，y)，则该等边三角形的边长为2y，故其面积等于
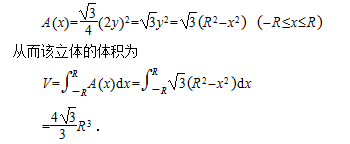
答案仅供参考，不要直接抄袭哦
相似问题
利用定积分概念求下列极限：(1)lim(n→＋∞)(1／((n＋1)＋1／(n＋2)＋...＋1／2
利用定积分概念求下列极限：(1)lim(n→＋∞)(1／((n＋1)＋1／(n＋2)＋ ＋1／2n)利用定积分概念求下列极限：
逻辑斯谛(Logistic)曲线族y=A／(1＋Be－cs:－∞
逻辑斯谛(Logistic)曲线族y=A／(1＋Be－cs:－∞
求由方程∫y 0 e^tdt＋∫x 0 cos tdt=0.所确定的隐函数y=y(x)的导数.求由方
求由方程∫y 0 e^tdt＋∫x 0 cos tdt=0 所确定的隐函数y=y(x)的导数 求由方程所确定的隐函数y=y(x)的导数
用比较审敛法判别下列级数的敛散性．(1)1／(4.6)＋(1／5.7)＋...＋1／(n＋3)(n＋
用比较审敛法判别下列级数的敛散性．(1)1／(4 6)＋(1／5 7)＋ ＋1／(n＋3)(n＋5)＋ 用比较审敛法判别下列级数的敛散性．
判定下列级数是否收敛？若收敛 是绝对收敛还是条件收敛？(1)1－1／√2＋1／√3－1／√4＋...
判定下列级数是否收敛？若收敛，是绝对收敛还是条件收敛？(1)1－1／√2＋1／√3－1／√4＋ 判定下列级数是否收敛？若收敛，是绝对收敛还是条件收敛？
