设u1 u2u3 u4 u5各点之间的距离表如下： 求由某一点出发 遍历每个点各一次 最后又返回出

正确答案：(1)距离矩阵的各行分别减去该行的最小数各列也分别减去该列的最小数得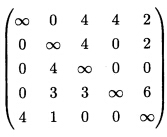：(2)求最优路径： (i)从第一行开始依次检查找出只有一个0元素没有加标记的行给这个0元素加标记“*”与这个加标记“0”同列的0元素全划去。重复此过程直到每一行没有未加标记的0元素或至少有两个未加标记的0。(ii)从第一列开始依次检查各列找出只有一个未加标记的0元素的列将这个0元素加上标记“*”并将与这个“0”同行的0元素全划去。重复此过程直到每一列没有尚未加标记的0或者至少有两个未加标记的0元素。(iii)重复(i)(ii)直到矩阵中没有未加标记的0元素为止。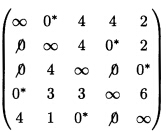由上面的矩阵可以看出：v₁→v₂ v₂→v₄v₄→v₁v₃→v₅v₅→v₃总距离为：2+4+2+2+5=15 (3)打开节点个数少的环路令d₃₅=∞或d₅₃=∞调整过程如下：(i)令d₃₅=∞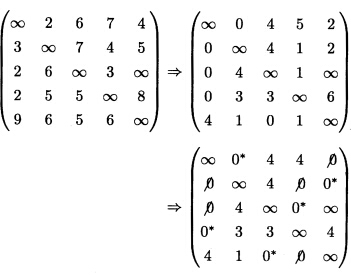可得：v₁→v₂→v₅→v₃→v₄→v₁无环路于是总距离为：2+5+3+2+5=17(ii)令d₅₃=∞得得路径v₁→v₂→v₁v₃→v₅→v₄→v₃总路径为：2+3+2+5+6=18若再打开节点最少得环路求解其点距离必大于或等于18故无需再计算了。所以最优路径为：v₁→v₂→v₅→v₃→v₄→v₁总距离为17。
(1)距离矩阵的各行分别减去该行的最小数,各列也分别减去该列的最小数得：(2)求最优路径：(i)从第一行开始依次检查,找出只有一个0元素没有加标记的行,给这个0元素加标记“*”,与这个加标记“0”同列的0元素全划去。重复此过程,直到每一行没有未加标记的0元素或至少有两个未加标记的0。(ii)从第一列开始依次检查各列,找出只有一个未加标记的0元素的列,将这个0元素加上标记“*”,并将与这个“0”同行的0元素全划去。重复此过程,直到每一列没有尚未加标记的0或者至少有两个未加标记的0元素。(iii)重复(i),(ii),直到矩阵中没有未加标记的0元素为止。由上面的矩阵可以看出：v1→v2v2→v4,v4→v1,v3→v5,v5→v3总距离为：2+4+2+2+5=15(3)打开节点个数少的环路,令d35=∞或d53=∞,调整过程如下：(i)令d35=∞,可得：v1→v2→v5→v3→v4→v1无环路,于是总距离为：2+5+3+2+5=17(ii)令d53=∞,得得路径v1→v2→v1,v3→v5→v4→v3总路径为：2+3+2+5+6=18若再打开节点最少得环路求解,其点距离必大于或等于18,故无需再计算了。所以最优路径为：v1→v2→v5→v3→v4→v1总距离为17。