设二维随机变量(X Y)的分布律为 P{X=m Y=n}=p2qn 0＜p＜1 q=1一p m=1
设二维随机变量(X，Y)的分布律为 P{X=m，Y=n}=p2qn，0＜p＜1，q=1一p，m=1，2，…，n=m+1，m+2，…，求条件分布律．
请帮忙给出正确答案和分析，谢谢！
参考解答
45j***444
2023-11-13 16:56:39
正确答案：先求边缘分布律对取定的m=12…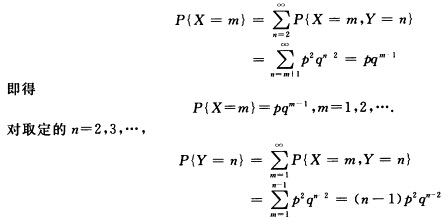
即得 P{Y=n=(n—1)p2qn—2n=23…． 下面求条件分布律当X=m=12…时
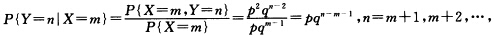即得在X=m的条件下Y的条件分布律为 P{Y=n｜X=m=pqn—m—1n=m+1m+2…．当Y=n=23…时
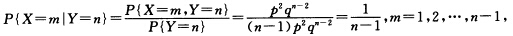即得在Y=n的条件下X的条件分布律为 P{X=m｜Y=n=
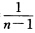n=12…n一1．
为求条件分布律，首先求边缘分布律，这可用下面的式子计算：．然后用下面的式子计算条件分布律：．在上面的计算中注意：只有当n≥m+1时，才有P{X=m，Y=n)=p2qn—2，否则P{X=m，Y=n=0．
相似问题
设连续型随机变量X的概率密度为 求E(X)N D(X)．请帮忙给出正确答案和分析 谢谢！
设连续型随机变量X的概率密度为，求E(X)N D(X)．请帮忙给出正确答案和分析，谢谢！
某人有M把伞 并在办公室和家之间往返．如果某天他在家中(办公室时)下雨而且家中(办公室)有伞他就带一
某人有M把伞，并在办公室和家之间往返．如果某天他在家中(办公室时)下雨而且家中(办公室)有伞他就带一把伞去上班(回家)，不下雨时他从不带伞．如果每天与
迷宫问题．将小家鼠放入迷宫中做动物的学习试验 如图6．6所示．在迷宫的第7号小格内放有美味食品而第8
迷宫问题．将小家鼠放入迷宫中做动物的学习试验，如图6．6所示．在迷宫的第7号小格内放有美味食品而第8号小格内则是电击捕鼠装置，假定当家鼠位于某格时
考虑三个状态E={0 1 2}的马尔可夫链{Xn n≥0} 其转移概率矩阵为 其中p q r＞0
考虑三个状态E={0，1，2}的马尔可夫链{Xn，n≥0}，其转移概率矩阵为 其中p，q，r＞0，p+q+r=1．这一马尔可夫链从状态1开始，一旦进入状态0或2就无法跳
若随机过程X(t)的样本函数可用傅氏级数表示为 其中t0是在一个周期内均匀分布的随机变量 an b
若随机过程X(t)的样本函数可用傅氏级数表示为 其中t0是在一个周期内均匀分布的随机变量，an，bn是常数，试求出X(t)的功率谱密度．请帮忙给出正确答案
