考虑三个状态E={0 1 2}的马尔可夫链{Xn n≥0} 其转移概率矩阵为 其中p q r＞0
考虑三个状态E={0，1，2}的马尔可夫链{Xn，n≥0}，其转移概率矩阵为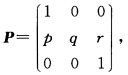 
其中p，q，r＞0，p+q+r=1．这一马尔可夫链从状态1开始，一旦进入状态0或2就无法跳出(称0，2为吸收态)．试求： (1)假如过程从状态1出发，则被状态0(或2)吸收的概率是多少? (2)平均要多么长的时间，过程会进入吸收态(而永远停在那里)?
请帮忙给出正确答案和分析，谢谢！
参考解答
42j***444
2023-11-13 16:09:26
正确答案：设T为过程进入吸收态的时刻它显然是一个随机变量且 T=min{n：Xn=0或2)则 u=P{“从状态1出发最终进入吸收态0”
设T为过程进入吸收态的时刻,它显然是一个随机变量,且T=min{n：Xn=0或2),则u=P{“从状态1出发最终进入吸收态0”
相似问题
若随机过程X(t)的样本函数可用傅氏级数表示为 其中t0是在一个周期内均匀分布的随机变量 an b
若随机过程X(t)的样本函数可用傅氏级数表示为 其中t0是在一个周期内均匀分布的随机变量，an，bn是常数，试求出X(t)的功率谱密度．请帮忙给出正确答案
设(X1 X2 … Xn)为来自正态总体N(μ σ2)的样本 为其样本均值 今 请帮忙给出正确答案
设(X1，X2，…，Xn)为来自正态总体N(μ，σ2)的样本，为其样本均值，今 请帮忙给出正确答案和分析，谢谢！
设(X1 X2 … Xn)和(Y1 Y2 … Yn)是分别来自正态总体N(1 σ2)和N(2 σ2)
设(X1，X2，…，Xn)和(Y1，Y2，…，Yn)是分别来自正态总体N(1，σ2)和N(2，σ2)的两个独立样本，与S12分别为(X1，X2，…，Xn)的样本均值和样本方差，与S2
设(X1 X2 … X5)是来自正态总体N(2．5 62)的样本 S2是其样本均值与样本方差 求概
设(X1，X2，…，X5)是来自正态总体N(2．5，62)的样本，，S2是其样本均值与样本方差，求概率P{(1．3＜＜3．5)∩(6．3＜S2＜9．6))．请帮忙给出正确答案和分析，谢谢！
设X(t)为一个二元波过程 它的一个样本函数如图7．3所示 已知在每个单位长’度的日寸间间隔内波形取
设X(t)为一个二元波过程，它的一个样本函数如图7．3所示，已知在每个单位长’度的日寸间间隔内波形取正、负值的概率各为，假定任一间隔内波形的取值与任
