用一块半径为r的圆形铁皮 剪去一圆心角为a的扇形 把余下部分围成一个圆锥．问a为何值时 圆锥的容积最
用一块半径为r的圆形铁皮，剪去一圆心角为a的扇形，把余下部分围成一个圆锥．问a为何值时，圆锥的容积最大(图4—2所示)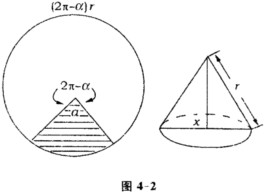
请帮忙给出正确答案和分析，谢谢！
参考解答
456***100
2024-11-07 15:23:51
正确答案：该问题的目标是容积V最大出于圆锥的斜高就足网形铁皮的半径r它是定值因此．V只依赖于底面半径x由x便可确定a．设圆锥底面半径为x容积为V．
该问题的目标是容积V最大,出于圆锥的斜高就足网形铁皮的半径r它是定值,因此．V只依赖于底面半径x,由x便可确定a．设圆锥底面半径为x,容积为V．
相似问题
证明：(1)可导的偶函数的导数是奇函数； (2)可导的奇函数的导数是偶函数； (3)可导的周期函数的
证明：(1)可导的偶函数的导数是奇函数； (2)可导的奇函数的导数是偶函数； (3)可导的周期函数的导数是具有相同周期的周期函数．请帮忙给出正确答案和分
下列曲线中有拐点(0 0)的是[ ]．A．y＝x2B．y＝x3C．y＝x4D．y＝x2／3请帮忙给出
下列曲线中有拐点(0，0)的是[ ]．A．y＝x2B．y＝x3C．y＝x4D．y＝x2／3请帮忙给出正确答案和分析，谢谢！
将曲线y＝1－x2(0≤x≤1)和x轴与y轴所围的区域用曲线y＝ax2分为面积相等的两部分 其中a是
将曲线y＝1－x2(0≤x≤1)和x轴与y轴所围的区域用曲线y＝ax2分为面积相等的两部分，其中a是大于零的常数，求a的值．请帮忙给出正确答案和分析，谢谢！
判定下列级数哪些是绝对收敛 哪些是条件收敛： 请帮忙给出正确答案和分析 谢谢！
判定下列级数哪些是绝对收敛，哪些是条件收敛： 请帮忙给出正确答案和分析，谢谢！
方程y－xey＝1确定y是x的函数 求y〞｜x＝0．请帮忙给出正确答案和分析 谢谢！
方程y－xey＝1确定y是x的函数，求y〞｜x＝0．请帮忙给出正确答案和分析，谢谢！
