求函数u＝x2＋y2＋z2在约束条件z＝x2＋y2和x＋y＋z＝4下的最大值与最小值．请帮忙给出正确
求函数u＝x2＋y2＋z2在约束条件z＝x2＋y2和x＋y＋z＝4下的最大值与最小值．
请帮忙给出正确答案和分析，谢谢！
参考解答
456***101
2024-11-08 17:40:22
正确答案：设拉格朗日函数为 F(xyz)＝x2＋y2＋z2＋λ(z－x2－y2)＋μ(x＋y＋z－4)解方程组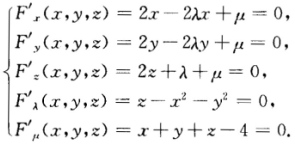
得
故最大值、最小值分别为umax＝(－2)2＋(－2)2＋82＝72umin＝12－12＋12
本题考查两个约束条件下的函数u＝f(x，y，x)的条件极值问题，可类似地构造拉格朗日函数F(x，y，z，λ，μ)＝f(x，y，z)＋λψ(x，y，z)＋μψ(x，y，z)解出可能极值点后，直接代入目标函数计算函数值再比较大小确定相应的极值(或最值)即可．
相似问题
设一平面通过从点(1 －1 1)到直线的垂线 且与平面z＝0垂直 求此平面的方程．请帮忙给出正确答案
设一平面通过从点(1，－1，1)到直线的垂线，且与平面z＝0垂直，求此平面的方程．请帮忙给出正确答案和分析，谢谢！
二元函数f(x y)在点(0 0)处可微的一个充分条件是A．B．C．D．请帮忙给出正确答案和分析 谢
二元函数f(x，y)在点(0，0)处可微的一个充分条件是A．B．C．D．请帮忙给出正确答案和分析，谢谢！
设Mo是直线L外的一点 M是直线上的任意一点 且直线L的方向向量为s 证明：Mo到直 请帮忙给出正确
设Mo是直线L外的一点，M是直线上的任意一点，且直线L的方向向量为s，证明：Mo到直 请帮忙给出正确答案和分析，谢谢！
设u＝f(x y z)有连续的一阶偏导数 又函数y＝y(x)及z＝z(x)分别由下列两式确定： 求
设u＝f(x，y，z)有连续的一阶偏导数，又函数y＝y(x)及z＝z(x)分别由下列两式确定： 求。请帮忙给出正确答案和分析，谢谢！
求f(x y)＝x2＋2y2－x2y2在区域D＝{(x y)｜x2＋y2≤4 y≥0)上的最大值和最
求f(x,y)＝x2＋2y2－x2y2在区域D＝{(x，y)｜x2＋y2≤4，y≥0)上的最大值和最小值．请帮忙给出正确答案和分析，谢谢！
