设三阶方阵A的特征值为2 1 一1 且其对应的特征向量分别为(1 0 一1) (1 一1 0) (1
设三阶方阵A的特征值为2，1，一1，且其对应的特征向量分别为(1，0，一1)，(1，一1，0)，(1，0，1)．求A=?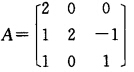
请帮忙给出正确答案和分析，谢谢！
参考解答
456***101
2024-11-13 11:42:55
正确答案：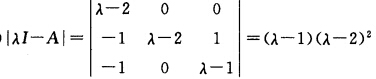
故A的特征根为：λ1=1λ2=λ3=2．对应于λ1=1解方程组 (1.I—A)X=0可得一基础解系为：
又对应于α2=α=32解方程组(2I一A)X=0即可得一基础解系为：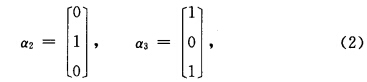
于是α1α2α3为三个线性无关的特征向量从而A可以对角化．令P为以α1α2α3为列的矩阵即
故A的特征根为：λ1=1,λ2=λ3=2．对应于λ1=1,解方程组(1.I—A)X=0,可得一基础解系为：又对应于α2=α=32,解方程组(2I一A)X=0,即可得一基础解系为：于是α1,α2,α3为三个线性无关的特征向量,从而A可以对角化．令P为以α1,α2,α3为列的矩阵,即
相似问题
设y＝ln cos x2；y＝ln cos x2；请帮忙给出正确答案和分析 谢谢！
设y＝ln cos x2；y＝ln cos x2；请帮忙给出正确答案和分析，谢谢！
微分方程y'＋2y＝0的通解是_______．请帮忙给出正确答案和分析 谢谢！
微分方程y "＋2y＝0的通解是_______．请帮忙给出正确答案和分析，谢谢！
设实二次型f(x1 x2 … xn)=l+…+l1一ls+1一…一ls+u 其中li(i=1 2 …
设实二次型f(x1，x2，…，xn)=l+…+l1一ls+1一…一ls+u，其中li(i=1，2，…，s+u)是x1，x2，…，xn的1次齐次多项式．证明；f(x1，x请帮忙给出正确答案和分析，谢谢！
某年某市对1 000户居民的抽样调查结果表明 全年居民购买副食品支出占购买食品支出的75．4％ 试以
某年某市对1 000户居民的抽样调查结果表明，全年居民购买副食品支出占购买食品支出的75．4％，试以99％的概率估计全年这种比率的置信区间．请帮忙给出正
设函数f(x)在x0处的导数不存在 则曲线y＝f(x)( )．A．在点(x0 f(x0))的切线必不
设函数f(x)在x0处的导数不存在，则曲线y＝f(x)( )．A．在点(x0，f(x0))的切线必不存在B．在点(x0，f(x0))的切线可能存在C．在x0处间断D．不存在此题为多
