在“充分而非必要” “必要而非充分”和“充分必要”三者中选择一个正确的填人下列空格内： (1)f(x
在“充分而非必要”、“必要而非充分”和“充分必要”三者中选择一个正确的填人下列空格内： (1)f(x)在点x。连续是f(x)在点x。可导的__________条件； (2)f(x)在点x。的左导数fˊ－(x。)及右导数fˊ＋＝(x。)都存在且相等是f(x)在点x。可导的_________条件； (3)f(x)在点x。可导是f(x)在点x。可微的__________条件； (4)对可导函数f(x)而言，x。为f(x)的驻点是x。为f(x)的极值点的_________条件； (5)fˊ(x)在[a，b]上恒大于零是f(x)在[a，b]上单调增加的__________条件； (6)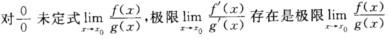
存在的_________条件．
请帮忙给出正确答案和分析，谢谢！
参考解答
456***101
2024-11-09 21:38:23
正确答案：
相似问题
证明下列导数公式： (1)(cotx)ˊ＝－csc2x； (2)(cscx)ˊ＝－cotx·cscx
证明下列导数公式： (1)(cotx)ˊ＝－csc2x； (2)(cscx)ˊ＝－cotx·cscx； 请帮忙给出正确答案和分析，谢谢！
汽车连同载重共5t 在抛物线拱桥上行驶 速度为21．6 km／h 桥的跨度为10 m 拱的矢高为0．
汽车连同载重共5t，在抛物线拱桥上行驶，速度为21．6 km／h，桥的跨度为10 m，拱的矢高为0．25 m(如图2．13所示)．求汽车越过桥顶时对桥的压力．请帮
甲 乙两地相距skm 汽车从甲地匀速地行驶到乙地 已知汽车每小时的运输成本(以元为单位)由可变部分与
甲、乙两地相距skm，汽车从甲地匀速地行驶到乙地，已知汽车每小时的运输成本(以元为单位)由可变部分与固定部分组成：可变部分与速度(单位为km／h)的平方
试用Mathematica求出下列函数的导数： (1)y＝sinx3； (2)y＝arctan(1n
试用Mathematica求出下列函数的导数： (1)y＝sinx3； (2)y＝arctan(1nx)； (3)y＝(1＋1／x)x； (4)y＝2xf(x2)．请帮忙给出正确答案和分析，谢谢！
在抛物线y＝x2上取横坐标为x1＝1及x2＝3的两点 作过这两点的割线．问该抛物线上哪一点的切线平行
在抛物线y＝x2上取横坐标为x1＝1及x2＝3的两点，作过这两点的割线．问该抛物线上哪一点的切线平行于这条割线?请帮忙给出正确答案和分析，谢谢！
