设函数y＝f(x)在区间[－1 3]上的图形如图1—3—14所示： 则函数F(x)＝∫0xf(t)d
设函数y＝f(x)在区间[－1，3]上的图形如图1—3—14所示： 则函数F(x)＝∫0xf(t)dt的图形为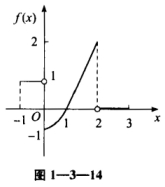 
A．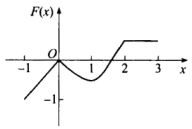
B．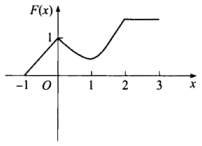
C．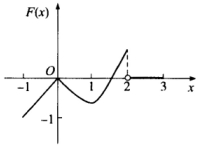
D．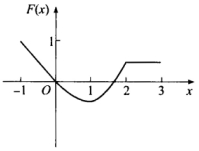
请帮忙给出正确答案和分析，谢谢！
参考解答
456***101
2024-11-09 20:46:59
正确答案：D
[分析此题考查定积分的应用知识．[详解由y＝f(x)的图形可见，其图象与x轴及y轴、x＝x0所围成的图形的代数面积为F(x0)，从而有①x∈[－1，0时，F(x)≤0为线性函数且单调递增．②x∈[0，1时，F(x)≤0且单调递减．③x∈[1，2时，F(x)单调递±曾．④x∈[2，3时，F(x)为常函数．⑤F(x)是连续函数．可见正确选项为(D)．[评注此题较新颖，给出函数f(x)的图形，讨论变限积分函数F(x)的图形．
相似问题
函数f(x)在[0 ＋∞)上可导 f(0)＝1 且满足等式 。 (1)求导数f(x)； (2)证明：
函数f(x)在[0，＋∞)上可导，f(0)＝1，且满足等式 。 (1)求导数f(x)； (2)证明：当x≥0时，不等式e－x≤f(x)≤1成立．请帮忙给出正确答案和分析，谢谢！
设曲线方程为y＝e－x(x≥0)． (1)把曲线y＝e－x(x≥0) x轴 y轴和直线x＝ξ(ξ＞0
设曲线方程为y＝e－x(x≥0)． (1)把曲线y＝e－x(x≥0)，x轴，y轴和直线x＝ξ(ξ＞0)所围成平面图形绕x轴旋转一周，得一旋转体，求此旋转体的体积V(ξ)，
设函数f(x)在(－∞ ＋∞)内连续 且F(x)＝∫0x(x－2t)f(t)dt 试证： (1)若f
设函数f(x)在(－∞，＋∞)内连续，且F(x)＝∫0x(x－2t)f(t)dt，试证： (1)若f(x)为偶函数，则F(x)也是偶函数； (2)若f(x)单调不增，则F(x)单调不减．请
设函数f(x)可导 且f(0)＝0 F(x)＝∫0xtn－1f(xn－tn)出 求.请帮忙给出正确答
设函数f(x)可导，且f(0)＝0，F(x)＝∫0xtn－1f(xn－tn)出，求 请帮忙给出正确答案和分析，谢谢！
当0≤θ≤π时 对数螺线r＝eθ的弧长为________．请帮忙给出正确答案和分析 谢谢！
当0≤θ≤π时，对数螺线r＝eθ的弧长为________．请帮忙给出正确答案和分析，谢谢！
