结合图2-1到图2-4 正确理解气体分子的速率分布和能量分布的规律。 请帮忙给出正确答案和分析 谢谢
结合图2-1到图2-4,正确理解气体分子的速率分布和能量分布的规律。 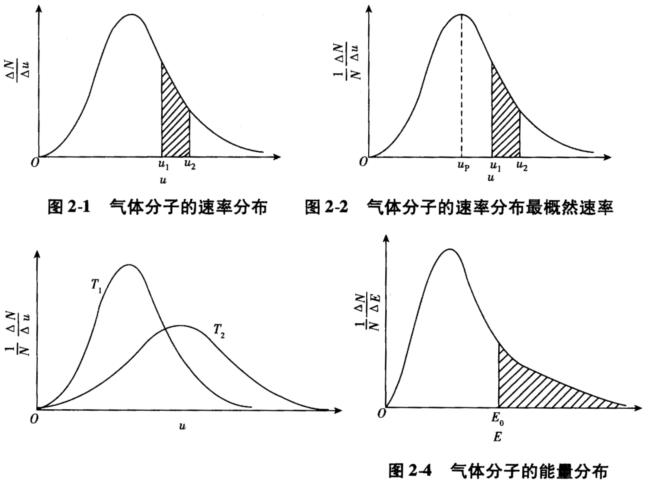
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:英国物理学家Maxwell对气体分子运动速率分布的研究结果表明速率极大和速率极小的分子都较少而速率居中的分子较多。图2-1表明了这一结果。纵坐标ΔN/Δu表示单位速率间隔内分子的数目;横坐标u代表分子的运动速率。曲线下覆盖的面积为分子的数目N阴影部分的面积为速率在u1和u2之间的气体分子的数目。从图中可以看出速率大的分子数目少速率小的分子数目也少速率居中的分子数目较多。图2-1的不足之处在于面积代表的是一个绝对的数量N因而气体分子总数不同时图形会有不同。若将纵坐标改为(1 ΔN)/(N Δu)其中N为分子总数对u作图见图2-2则曲线下覆盖的面积将是某速率区间内分子数占分子总数的分数ΔN/N。而曲线下u1和u2之间阴影部分的面积表示速率处于u1和u2之间的气体分子的数目占分子总数的分数。由此可知整个曲线下覆盖的总面积为单位1。 这种分布曲线的优点在于只要温度相同无论气体分子的总数怎样变化曲线形状保持一致。 如图2-3温度升高时气体分子的运动速度普遍增大具有较高速率的分子的分数必然提高分布曲线右移。最概然速率up也随温度的升高而变大但具有这种速率的分子的分数却变小了。由于曲线下覆盖的面积为定值故高度降低的同时曲线覆盖面加宽整个曲线变得较为平坦。气体分子的能量受其速率的影响因此能量的分布与速率分布相类似见图2-4。与速率分布不同的是能量分布曲线上升阶段较陡下降的后一阶段趋于平缓。 在无机化学中常用近似公式来计算和讨论能量的分布: fE0=Ni/N=e-E0/(RT)式中E0是某个特定的能量数值;Ni/N表示能量大于E0的分子占所有分子的分数从式中可以看出E0越大fE0越小。
英国物理学家Maxwell对气体分子运动速率分布的研究结果表明,速率极大和速率极小的分子都较少,而速率居中的分子较多。图2-1表明了这一结果。纵坐标ΔN/Δu表示单位速率间隔内分子的数目;横坐标u代表分子的运动速率。曲线下覆盖的面积为分子的数目N,阴影部分的面积为速率在u1和u2之间的气体分子的数目。从图中可以看出,速率大的分子数目少,速率小的分子数目也少,速率居中的分子数目较多。图2-1的不足之处在于,面积代表的是一个绝对的数量N,因而气体分子总数不同时,图形会有不同。若将纵坐标改为(1ΔN)/(NΔu),其中N为分子总数,对u作图,见图2-2,则曲线下覆盖的面积,将是某速率区间内分子数占分子总数的分数ΔN/N。而曲线下u1和u2之间阴影部分的面积表示速率处于u1和u2之间的气体分子的数目占分子总数的分数。由此可知整个曲线下覆盖的总面积为单位1。这种分布曲线的优点在于,只要温度相同,无论气体分子的总数怎样变化,曲线形状保持一致。如图2-3,温度升高时,气体分子的运动速度普遍增大,具有较高速率的分子的分数必然提高,分布曲线右移。最概然速率up也随温度的升高而变大,但具有这种速率的分子的分数却变小了。由于曲线下覆盖的面积为定值,故高度降低的同时,曲线覆盖面加宽,整个曲线变得较为平坦。气体分子的能量受其速率的影响,因此能量的分布与速率分布相类似,见图2-4。与速率分布不同的是能量分布曲线上升阶段较陡,下降的后一阶段趋于平缓。在无机化学中,常用近似公式来计算和讨论能量的分布:fE0=Ni/N=e-E0/(RT)式中,E0是某个特定的能量数值;Ni/N表示能量大于E0的分子占所有分子的分数,从式中可以看出,E0越大,fE0越小。
相似问题
通过直线设f(x y z)=exyz2 其中z=z(x y)是由x+y+z+xyz=0确定的隐函数
通过直线设f(x,y,z)=exyz2,其中z=z(x,y)是由x+y+z+xyz=0确定的隐函数,则fz(0,1,一1)=_____.设f(x,y,z)=exyz2,其中z=z(x,y)是由x+y+z+xyz=
设曲线L上位于xOy平面第一象限内任意一点M处的切线总与y轴相交 交点为A 已知 且曲线L为过点(3
设曲线L上位于xOy平面第一象限内任意一点M处的切线总与y轴相交,交点为A,已知,且曲线L为过点(3/2,3/2),求曲线L的方程.请帮忙给出正确答案和分析,谢谢!
在讨论供求关系时 某商品的需求量 供给量和价格均被看作时间n的函数 n取整数型离散值.传统的基本动态
在讨论供求关系时,某商品的需求量、供给量和价格均被看作时间n的函数,n取整数型离散值.传统的基本动态供需均衡模型为 模型表明,现期需求依赖于同
某养鱼池最多能养1 000条鱼 鱼数y是t的函数 且鱼的数目的变化速度与y及1 000-y乘积成正比
某养鱼池最多能养1 000条鱼,鱼数y是t的函数,且鱼的数目的变化速度与y及1 000-y乘积成正比,现知养鱼100条,3个月后变为250条,求函数y(t)以及6个月
用所给变换 将下列微分方程化为变量可分离方程或线性方程 并求解方程: 请帮忙给出正确答案和分析 谢谢
用所给变换,将下列微分方程化为变量可分离方程或线性方程,并求解方程: 请帮忙给出正确答案和分析,谢谢!












