某厂商有两个工厂生产同一产品。第一个工厂生产函数为y1=min( x2) 第二个工厂的生产函数为y2
某厂商有两个工厂生产同一产品。第一个工厂生产函数为y1=min(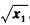 ,x2),第二个工厂的生产函数为y2={min(2x3+x4,x5)}1/4{min(x6,2x7)}1/4,其中x1—x7是生产所需的7种可变生产要素。工厂1和工厂2还各自需要5单位和10单位某种固定要素x8,8种生产要素的价格分别为:w1=1,w2=4,w3=2,w4=2,w5=1,w6=1,w7=2,w8=2。求: (1)两个工厂对7种可变生产要素的条件要素需求函数及各自的成本函数。(2)该厂商的总成本函数。(上海交通大学2011研)
,x2),第二个工厂的生产函数为y2={min(2x3+x4,x5)}1/4{min(x6,2x7)}1/4,其中x1—x7是生产所需的7种可变生产要素。工厂1和工厂2还各自需要5单位和10单位某种固定要素x8,8种生产要素的价格分别为:w1=1,w2=4,w3=2,w4=2,w5=1,w6=1,w7=2,w8=2。求: (1)两个工厂对7种可变生产要素的条件要素需求函数及各自的成本函数。(2)该厂商的总成本函数。(上海交通大学2011研)
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)分析工厂1的生产函数要素x1和x2互补且满足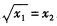 。因此生产函数变为
。因此生产函数变为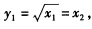 对应有x1=y12x2=y1此即工厂1对要素x1和x2的需求函数。 工厂1的成本函数为c1=w1x1+w2x2+w8x8=y12+4y1+10。 分析工厂2的生产函数首先看要素x3和x4是完全替代的替代比率为2:1即1单位x3可以替代2单位的x4而1单位的x3的成本为22单位的x4的成本为4所以工厂2对要素x4的条件需求为0因此工厂2的生产函数实际上可以写成如下形式: y2={min(2x3x5)1/4#.{min(x62x7)1/4 其中要素x3和x5是互补的关系且满足2x3=x5要素x6和x7也是互补的关系且满足x6=2x7因此工厂2的生产函数不妨写成y2=x51/4x63/4该生产函数下成本最小化的条件
对应有x1=y12x2=y1此即工厂1对要素x1和x2的需求函数。 工厂1的成本函数为c1=w1x1+w2x2+w8x8=y12+4y1+10。 分析工厂2的生产函数首先看要素x3和x4是完全替代的替代比率为2:1即1单位x3可以替代2单位的x4而1单位的x3的成本为22单位的x4的成本为4所以工厂2对要素x4的条件需求为0因此工厂2的生产函数实际上可以写成如下形式: y2={min(2x3x5)1/4#.{min(x62x7)1/4 其中要素x3和x5是互补的关系且满足2x3=x5要素x6和x7也是互补的关系且满足x6=2x7因此工厂2的生产函数不妨写成y2=x51/4x63/4该生产函数下成本最小化的条件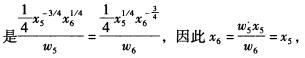 代入生产函数可得对要素x5和x6的需求函数为x5=x6=y22易得要素x3和x7的需求函数为
代入生产函数可得对要素x5和x6的需求函数为x5=x6=y22易得要素x3和x7的需求函数为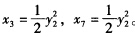 因此工厂2的成本函数为c=w3x3+w5x5+w6x6+w7x7+w8x8=4y22+20。 (2)因为产品相同所以两个工厂的边际成本应该相同为此有MC1=2y1+4=MC2=8y2。设总产量为y因此有y=y1+y2于是有y1=0.8y—0.4和y2=0.2y+0.4于是该厂商的总成本函数c=c1+c2=(0.8y一0.4)2+4(0.8y一0.4)+10+4(0.2y+0.4)2+20=0.8y2+3.2y+30.64。
因此工厂2的成本函数为c=w3x3+w5x5+w6x6+w7x7+w8x8=4y22+20。 (2)因为产品相同所以两个工厂的边际成本应该相同为此有MC1=2y1+4=MC2=8y2。设总产量为y因此有y=y1+y2于是有y1=0.8y—0.4和y2=0.2y+0.4于是该厂商的总成本函数c=c1+c2=(0.8y一0.4)2+4(0.8y一0.4)+10+4(0.2y+0.4)2+20=0.8y2+3.2y+30.64。
(1)分析工厂1的生产函数,要素x1和x2互补,且满足。因此生产函数变为,对应有x1=y12,x2=y1,此即工厂1对要素x1和x2的需求函数。工厂1的成本函数为c1=w1x1+w2x2+w8x8=y12+4y1+10。分析工厂2的生产函数,首先看要素x3和x4是完全替代的,替代比率为2:1,即1单位x3可以替代2单位的x4,而1单位的x3的成本为2,2单位的x4的成本为4,所以工厂2对要素x4的条件需求为0,因此工厂2的生产函数实际上可以写成如下形式:y2={min(2x3,x5)1/4#.{min(x6,2x7)1/4其中要素x3和x5是互补的关系,且满足2x3=x5,要素x6和x7也是互补的关系,且满足x6=2x7,因此工厂2的生产函数不妨写成y2=x51/4x63/4,该生产函数下成本最小化的条件代入生产函数可得对要素x5和x6的需求函数为x5=x6=y22,易得要素x3和x7的需求函数为因此工厂2的成本函数为c=w3x3+w5x5+w6x6+w7x7+w8x8=4y22+20。(2)因为产品相同,所以两个工厂的边际成本应该相同,为此有MC1=2y1+4=MC2=8y2。设总产量为y,因此有y=y1+y2,于是有y1=0.8y—0.4和y2=0.2y+0.4,于是该厂商的总成本函数c=c1+c2=(0.8y一0.4)2+4(0.8y一0.4)+10+4(0.2y+0.4)2+20=0.8y2+3.2y+30.64。
相似问题
他们均衡价格 各自的均衡产量和利润;请帮忙给出正确答案和分析 谢谢!
他们均衡价格、各自的均衡产量和利润;请帮忙给出正确答案和分析,谢谢!
如果MPL/MPK>w/r 其中 MPL:劳动边际产量;MPk:资本边际产量;w:工资;r:利润。那
如果MPL/MPK>w/r,其中,MPL:劳动边际产量;MPk:资本边际产量;w:工资;r:利润。那就应该( )。(上海财经大学2003研)A.用更多的劳动替代资本B.
某一行业的寡头企业在市场上以共谋形式从事经营活动 这在经济学上称为( )。(中山大学2003研)A.
某一行业的寡头企业在市场上以共谋形式从事经营活动,这在经济学上称为( )。(中山大学2003研)A.价格领先B.管制行业C.卡特尔D.不完全竞争请帮忙给出
某产品的市场需求曲线为P=880—4Q 其中P为价格 Q为总产量。假定行业内有两个企业 它们进行斯塔
某产品的市场需求曲线为P=880—4Q,其中P为价格,Q为总产量。假定行业内有两个企业,它们进行斯塔克尔伯格(Stackelberg)竞争。每个企业的边际成本为常数8
设对一垄断厂商的两种产品的需求函数如下: Q1=40一2P1+P2 Q2=15+P1一P2 该厂商的
设对一垄断厂商的两种产品的需求函数如下: Q1=40一2P1+P2 Q2=15+P1一P2 该厂商的总成本函数为: C=(Q1)2+Q1Q2+(Q2)2 请求出该厂商取得最大利润时的












