设函数f(x)在[a b]上连续 且在(a b)内有fˊ(x)＞0．证明：在(a b)内存在唯一的ε
设函数f(x)在[a，b]上连续，且在(a，b)内有fˊ(x)＞0．证明：在(a，b)内存在唯一的ε，使曲线y＝f(x)与两直线y＝f(ε)，x＝a所围平面图形面积s1是曲线y＝f(x)与两直线y＝f(ε)，x＝b所围平面图形面积S2的3倍．
请帮忙给出正确答案和分析，谢谢！
参考解答
432***102
2024-11-16 15:56:03
正确答案：证明 由f(x)在[ab上连续在(ab)内有fˊ(x)＞0可知f(x)在[ab上单调增加对于(ab)内任意一点t。作平行于x轴的直线y＝f(t)与曲线只交一点并与曲线y=f(x)直线x＝ax＝b分别围成平面图S1和S2如图6—22所示于是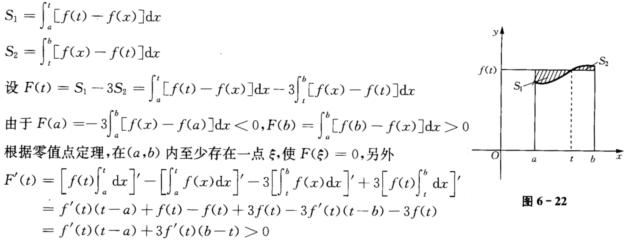
证明由f(x)在[a,b上连续,在(a,b)内有fˊ(x)＞0,可知f(x)在[a,b上单调增加,对于(a,b)内任意一点t。作平行于x轴的直线y＝f(t)与曲线只交一点,并与曲线y=f(x),直线x＝a,x＝b分别围成平面图S1和S2,如图6—22所示,于是
相似问题
已知函数f(x)在区间(1—δ 1+δ)内具有二阶导数 f'(x)
已知函数f(x)在区间(1—δ，1+δ)内具有二阶导数，f"(x)<0，且f(1)=f(1)=1，则( )．A．在(1—δ，1)和(1，1+δ)内均有f(x)<xB．在(1一δ，1)和(1，1+δ)
求下列递推公式(n为正整数)： 请帮忙给出正确答案和分析 谢谢！
求下列递推公式(n为正整数)： 请帮忙给出正确答案和分析，谢谢！
某厂生产某种产品的生产函数z＝20－x2＋10x－2y2＋5y 其中x和y为两种投入量 z为产出量．
某厂生产某种产品的生产函数z＝20－x2＋10x－2y2＋5y，其中x和y为两种投入量，z为产出量．若两种投入量的价格分别为2和1，产品的售价为5，试求最大利润．
设f(x)在R上有定义 证明：y＝f(x)的图形关于直线x＝1对称的充要条件是f(x)满足f(x+1
设f(x)在R上有定义，证明：y＝f(x)的图形关于直线x＝1对称的充要条件是f(x)满足f(x+1)＝f(1－x)，x∈R (2)设f(x)在R上有定义，且y＝f(x)的图形关于直线x
求下列隐函数的偏导数： 计算下列二重积分：计算下列二重积分： 请帮忙给出正确答案和分析 谢谢！
求下列隐函数的偏导数： 计算下列二重积分：计算下列二重积分： 请帮忙给出正确答案和分析，谢谢！
