证明：由平面上四个射影变换： 构成的集合G是一个变换群．请帮忙给出正确答案和分析 谢谢！
证明：由平面上四个射影变换：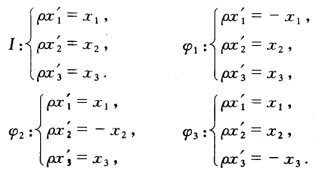 
构成的集合G是一个变换群．
请帮忙给出正确答案和分析，谢谢！
参考解答
420***102
2024-11-19 16:31:26
正确答案：此四个变换的乘积表如下：
由表可知：变换对乘积是封闭的． 又I-1＝Iφ1-1＝φ1φ2-1＝φ2φ3-1＝φ3所以每一个变换在G里都有逆变换因此G是一个变换群．
此四个变换的乘积表如下：由表可知：变换对乘积是封闭的．又I-1＝I,φ1-1＝φ1,φ2-1＝φ2,φ3-1＝φ3,所以每一个变换在G里都有逆变换,因此G是一个变换群．
相似问题
求点(2 －1 1)关于二级曲线4u12＋2u32＋u2u3＝0的极线．请帮忙给出正确答案和分析 谢
求点(2，－1，1)关于二级曲线4u12＋2u32＋u2u3＝0的极线．请帮忙给出正确答案和分析，谢谢！
设平面π内二点A B 二直线a b A B都不在a b上 平面π′内二点A′ B′ 二直线a′ b′
设平面π内二点A、B，二直线a，b，A，B都不在a，b上，平面π′内二点A′、B′，二直线a′、b′，A′、B′都不在a′、′上，问A、B分别对应A′，B′，a、b
设平面π内四点(0 0 1) (1 0 0) (－1 1 1) (1 1 0) 分别对应平面π′内四
设平面π内四点(0，0，1)，(1，0，0)，(－1，1，1)，(1，1，0)，分别对应平面π′内四点(1，－1，1)，(2，1，0)，(－2，0，1)，(1，3，0)，求射影对应，
设以坐标三点形的内心为单位点 求坐标三点形三个旁心的射影坐标．请帮忙给出正确答案和分析 谢谢！
设以坐标三点形的内心为单位点，求坐标三点形三个旁心的射影坐标．请帮忙给出正确答案和分析，谢谢！
求χ2＋y2＝r2的动切线关于aχ2＋by2＝1的极点的轨迹方程．请帮忙给出正确答案和分析 谢谢！
求χ2＋y2＝r2的动切线关于aχ2＋by2＝1的极点的轨迹方程．请帮忙给出正确答案和分析，谢谢！
