验证下列函数是否为所给方程的解(题中C1 C2 C3 C4为任意常数)： 试证函数y1(n)＝(－2

正确答案：将y₁(n)＝(－2)ⁿ代入方程的左端左端＝(－2)ⁿ⁺²＋4(－2)^n＋1＋4(－2)ⁿ＝(－2)ⁿ(4－8＋4)＝0＝右端 所以y₁(n)＝(－2)ⁿ为方程y_n＋2＋4y_n＋1＋4y_n＝0的解 将y₂(n)＝n(－2)ⁿ代入方程的左端 左端＝(n＋2)(－2)^n＋2＋4(n＋1)(－2)^n＋1＋4n(－2)ⁿ ＝(－2)ⁿ(4n＋8－8n－8＋4n)＝0＝右端 所以y₂(n)＝n(－2)ⁿ为方程y_n＋2＋4y_n＋1＋4y_n＝0的解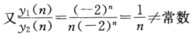所以y₁(n)与y₂(n)线性无关从而y₁(n)与y₂(n)是方程y_n+2＋4y_n＋1＋4y_n＝0的两个线性无关的解其通解为y_n＝C₁(－2)ⁿ＋C₂n(－2)ⁿ＝(－2)ⁿ(C₁＋C₂n)
将y1(n)＝(－2)n代入方程的左端,左端＝(－2)n+2＋4(－2)n＋1＋4(－2)n＝(－2)n(4－8＋4)＝0＝右端,所以y1(n)＝(－2)n为方程yn＋2＋4yn＋1＋4yn＝0的解将y2(n)＝n(－2)n代入方程的左端,左端＝(n＋2)(－2)n＋2＋4(n＋1)(－2)n＋1＋4n(－2)n＝(－2)n(4n＋8－8n－8＋4n)＝0＝右端,所以y2(n)＝n(－2)n为方程yn＋2＋4yn＋1＋4yn＝0的解,所以y1(n)与y2(n)线性无关,从而y1(n)与y2(n)是方程yn+2＋4yn＋1＋4yn＝0的两个线性无关的解,其通解为yn＝C1(－2)n＋C2n(－2)n＝(－2)n(C1＋C2n)