写出下列二次型的矩阵． 求一正交变换x=Py化二次型 为标准形；求一正交变换x=Py化二次型 为标准
写出下列二次型的矩阵． 求一正交变换x=Py化二次型，为标准形；
求一正交变换x=Py化二次型，为标准形；
请帮忙给出正确答案和分析，谢谢！
参考解答
420***101
2024-11-13 12:19:00
正确答案：由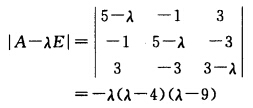
可得A的特征值为λ1=4λ2=9λ3=0．由(A—λE)X=0可求得490对应的特征向量为
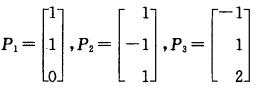对特征向量单位化得
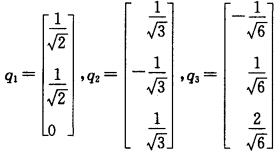故正交变换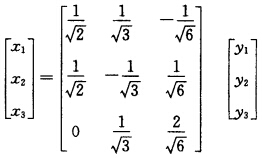
化二次型为f=4y12+9y22+0.y32
由可得A的特征值为λ1=4,λ2=9,λ3=0．由(A—λE)X=0可求得4,9,0对应的特征向量为对特征向量单位化得故正交变换化二次型为f=4y12+9y22+0.y32
相似问题
如图A B相似 试证A B的特征多项式相等。请帮忙给出正确答案和分析 谢谢！
如图A、B相似，试证A，B的特征多项式相等。请帮忙给出正确答案和分析，谢谢！
”阶行列式A的值为c 若将A的所有元素改变符号 得到的行列式值为( )．请帮忙给出正确答案和分析 谢
”阶行列式A的值为c，若将A的所有元素改变符号，得到的行列式值为( )．请帮忙给出正确答案和分析，谢谢！
写出下列二次型的矩阵． 指出方程f(x1 x2 x3)=1表示何种二次曲面．指出方程f(x1 x2
写出下列二次型的矩阵． 指出方程f(x1，x2，x3)=1表示何种二次曲面．指出方程f(x1，x2，x3)=1表示何种二次曲面．请帮忙给出正确答案和分析，谢谢！
若随机变量ξ的分布列如下表所示： 设θ是未知参数θ的一个估计 当________时 称θ是θ的无偏估
若随机变量ξ的分布列如下表所示： 设θ是未知参数θ的一个估计，当________时，称θ是θ的无偏估计．设θ是未知参数θ的一个估计，当________时，称θ
n级实对称矩阵A是半正定的充分必要条件为A的所有主子式全非负．请帮忙给出正确答案和分析 谢谢！
n级实对称矩阵A是半正定的充分必要条件为A的所有主子式全非负．请帮忙给出正确答案和分析，谢谢！
