写出下列二次型的矩阵． 设A是实对称矩阵 证明：当实数t充分分大之后 tE＋A是正定矩阵．设A是实对
写出下列二次型的矩阵． 设A是实对称矩阵，证明：当实数t充分分大之后，tE＋A是正定矩阵．
设A是实对称矩阵，证明：当实数t充分分大之后，tE+A是正定矩阵．
请帮忙给出正确答案和分析，谢谢！
参考解答
420***101
2024-11-13 13:01:46
正确答案：因为A是实对称矩阵则可推知A相似于对角矩阵即存在可逆矩阵P使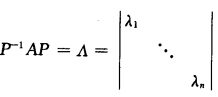
其中λi为实数那么A=PAP-1因为A为实对称矩阵所以tE+A民是实对称阵。取t>max)λi则P-1(tE+A)P=tE+P-1AP=tE+A=
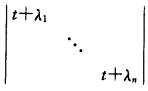因为t>maxλi则矩阵tE+A的任一特征值t+λi>0故tE+A当t>maxλi时为正定矩阵。
因为A是实对称矩阵,则可推知A相似于对角矩阵,即存在可逆矩阵P,使其中λi为实数,那么A=PAP-1,因为A为实对称矩阵,所以tE+A民是实对称阵。取t>max)λi,则P-1(tE+A)P=tE+P-1AP=tE+A=因为t>maxλi,则矩阵tE+A的任一特征值t+λi>0,故tE+A当t>maxλi时为正定矩阵。
相似问题
求下列微分方程的解：sec2x tan y dz＋sec2y tan x dy＝0 ；请帮忙给出正确
求下列微分方程的解：sec2x tan y dz＋sec2y tan x dy＝0，；请帮忙给出正确答案和分析，谢谢！
函数设f(x＋1)＝x2＋2x—5 则f(x)＝_______．设f(x＋1)＝x2＋2x—5 则f
函数设f(x＋1)＝x2＋2x—5，则f(x)＝_______．设f(x＋1)＝x2＋2x—5，则f(x)＝_______．请帮忙给出正确答案和分析，谢谢！
f(x1 x2 x3)=5x1+6x22+4x22一4x1x2—4x2x3；请帮忙给出正确答案和分析
f(x1，x2，x3)=5x1+6x22+4x22一4x1x2—4x2x3；请帮忙给出正确答案和分析，谢谢！
f(x1 x2 x3)=10x12+8x1x2+24x1x3+2x22一28x2x2+x2；请帮忙给
f(x1，x2，x3)=10x12+8x1x2+24x1x3+2x22一28x2x2+x2；请帮忙给出正确答案和分析，谢谢！
微分方程(y)2＋y(y')3＋xy4＝0的阶数是( )．A．1B．2C．3D．4此题为多项选择题。
微分方程(y)2＋y(y ")3＋xy4＝0的阶数是( )．A．1B．2C．3D．4此题为多项选择题。请帮忙给出正确答案和分析，谢谢！
