设X Y是离散型随机变量 其联合概率分布为P{X=xi Y=yj}=pij(i j=1 2 …) 边

参考解答

413***102

2024-11-20 07:11:57



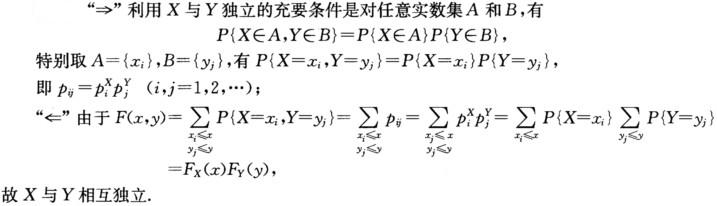
相似问题

• 函数F(x)=1/(1+x2)是否可作为某一随机变量的分布函数 如果 (1)-∞请帮忙给出正确答案和

  函数F(x)=1 (1+x2)是否可作为某一随机变量的分布函数，如果 (1)-∞请帮忙给出正确答案和分析，谢谢！

• 从清凉饮料自动售货机 随机抽样36杯 其平均含量为219(mL) 标准差为14．2mL 在α=0．0

  从清凉饮料自动售货机，随机抽样36杯，其平均含量为219(mL)，标准差为14．2mL，在α=0．05的显著性水平下，试检验假设： H0：μ0=222，H1：μ＜μ0222。

• 设F1(x)与F2(x)分别为任意两个随机变量的分布函数 令F(x)=aF1(x)+bF2(x) 则

  设F1(x)与F2(x)分别为任意两个随机变量的分布函数，令F(x)=aF1(x)+bF2(x)，则下列各组数中能使F(x)为某随机变量的分布函数的有( )．A．a=3 5，b=2 5B．a

• 设X服从(0 θ]上的均匀分布 X1 X2 … Xn 是取自总体X的一个简单随机样本 求θ的矩估计量

  设X服从(0，θ]上的均匀分布，X1，X2，…，Xn，是取自总体X的一个简单随机样本，求θ的矩估计量和最大似然估计量。请帮忙给出正确答案和分析，谢谢！

• 证明：射影平面的n条直线(其中任何三直线不共点)将平面分为证明：方程u12＋3u1u2－u22＝0所

  证明：射影平面的n条直线(其中任何三直线不共点)将平面分为证明：方程u12＋3u1u2－u22＝0所决定的两个证明：方程u12＋3u1u2－u22＝0所决定的两个无穷远点