证明：射影平面的n条直线(其中任何三直线不共点)将平面分为证明：方程u12＋3u1u2－u22＝0所
证明：射影平面的n条直线(其中任何三直线不共点)将平面分为证明：方程u12＋3u1u2－u22＝0所决定的两个
证明：方程u12＋3u1u2－u22＝0所决定的两个无穷远点在互相垂直的方向上．
请帮忙给出正确答案和分析，谢谢！
参考解答
432***102
2024-11-20 06:51:25
正确答案：分解因式可得：方程u12＋3u1u2－u22＝0所确定的二无穷远点之坐标为：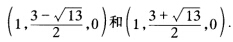
由于点的齐次坐标(1λ0)确定以λ为方向上的无穷远点而对于以上二无穷远点有
所以以上二无穷远点在互相垂直的方向上．
分解因式可得：方程u12＋3u1u2－u22＝0所确定的二无穷远点之坐标为：由于点的齐次坐标(1,λ,0)确定以λ为方向上的无穷远点,而对于以上二无穷远点有所以以上二无穷远点在互相垂直的方向上．
相似问题
要求一种元件平均使用寿命不得低于1 000小时 生产者从一批这种元件中随机抽取25件 测得其寿命的平
要求一种元件平均使用寿命不得低于1 000小时，生产者从一批这种元件中随机抽取25件，测得其寿命的平均值为950小时。已知该种元件寿命服从标准差为σ=100
对离散型情形证明：(1)E(X+Y)=EX+EY． (2)EXY=EXEY请帮忙给出正确答案和分析
对离散型情形证明：(1)E(X+Y)=EX+EY． (2)EXY=EXEY请帮忙给出正确答案和分析，谢谢！
设X1 X2 … Xn为来自正态总体N(μ σ2)的一个样本 求μ的置信度为1-α的单侧置信限。请帮
设X1，X2，…，Xn为来自正态总体N(μ，σ2)的一个样本，求μ的置信度为1-α的单侧置信限。请帮忙给出正确答案和分析，谢谢！
设(X Y)服从G={(x y)|0≤x≤2 0≤y≤1}上的均匀分布 求：X和Y的边缘密度函数.X
设(X，Y)服从G={(x，y)|0≤x≤2，0≤y≤1}上的均匀分布，求：X和Y的边缘密度函数 X和Y的边缘密度函数 请帮忙给出正确答案和分析，谢谢！
查表求t分布的下列上侧分位数：如t0.05(3) t0.01(5) t0.10(7)与t0.005(
查表求t分布的下列上侧分位数：如t0 05(3)，t0 01(5)，t0 10(7)与t0 005(10)。请帮忙给出正确答案和分析，谢谢！
