首页大学本科正文

第一类曲线积分的积分弧L是_________的(定向 不定向)；利用L的参数方程将这个积分化为定积分

大学本科 已帮助：人 时间:2024-11-08 01:50:58

第一类曲线积分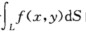
的积分弧L是_________的(定向、不定向)；利用L的参数方程将这个积分化为定积分时，下限α必须____________上限β． (2)第二类曲线积分
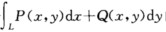的积分弧L是____________的(定向、不定向)；利用L的参数方程将这个积分化为定积分时，下限α对应_____________，上限β对应__________，α未必小于β． (3)第一类曲面积分
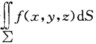的积分曲面∑是__________的(定向、不定向)；利用∑的方程z＝f(x，y)将这个积分化为二重积分时，曲面面积元素dS与二重积分面积元素曲的关系是_____________． (4)第二类曲面积分
的积分曲面∑是____________的(定向、不定向)；利用∑的方程z＝f(x，y)将这个积分化为二重积分时，曲面投影元素出dxdy与二重积分面积元素出的关系是_________，其中正负号根据____________来确定． (5)设P(x，y)、Q(x，y)均具有连续偏导数，则在平面___________区域内，曲线积分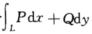
与路径无关的判别条件是____________． (6)格林公式、高斯公式和斯托克斯公式都是将一个在某个几何形体上的积分化为另一个在该几何形体的____________的积分，因此可看作是定积分中的____________公式的推广． (7)设c为椭圆x2／2＋y2／3＝1，其周长记为a，则
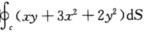＝___________. (8)设∑是一个球面，F是一个常向量场，则
＝__________. (9)设f(x，y，z)具有各阶连续偏导数，则div(rot▽f)＝___________．
请帮忙给出正确答案和分析，谢谢！

#站内搜索 #在百度搜 #在搜狗搜

难度：⭐⭐⭐

题库：大学本科,理学,数学类

标签：曲面,方程,积分

参考解答

用户头像

406***100

2024-11-08 01:50:58

正确答案：(1)不定向大于；(2)定向L的起点L的终点；(3)不定向；(4)dxdy＝±dδ∑的指向；(5)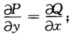；(6)边界上牛顿一莱布尼茨；(7)6a； (8)0； (9)0；
(1)不定向,大于；(2)定向,L的起点,L的终点；(3)不定向,；(4)dxdy＝±dδ,∑的指向；(5)；(6)边界上,牛顿一莱布尼茨；(7)6a；(8)0；(9)0；

上一篇 μ(x y)＝x2－xy＋y2 L为抛物线y＝x2自原点至点A(1 1)的有向弧段n为L的切向量顺时

下一篇 将下列函数展成麦克劳林级数： 请帮忙给出正确答案和分析 谢谢！

相似问题