求分式线性变换 w= ad—bc≠0 使扩充z平面上由三圆弧所围成的三角形与扩充w平面上的直线三角形

大学本科已帮助：人时间:2024-11-21 02:19:48

求分式线性变换 w=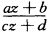
，ad—bc≠0 使扩充z平面上由三圆弧所围成的三角形与扩充w平面上的直线三角形相对应的充要条件．
请帮忙给出正确答案和分析，谢谢！

参考解答

406***102

2024-11-21 02:19:48



正确答案：必要性：若分式线性映射w=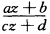使z平面上的由三圆弧所围成的三角形ABC与w平面上的直线三角形A'B'C'相对应时必有叫平面上的三直线通过w=∞点即三直线交于w=∞点因而对应的z平面上的三圆弧必交于一点z=一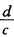(如图7—17)这就是必要条件．充分性：如果当w平面上的某三圆弧交于一点z=一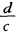时则三圆周在分式线性函数w=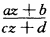映射下其像必是过w=∞点的三直线因而曲线三角形ABC被映射成直线三角形A'B'C'．即w平面上的某三圆周交于一点z=一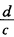也是三角形ABC映射成三角形A'B'C'的充分条件．
必要性：若分式线性映射w=使z平面上的由三圆弧所围成的三角形ABC与w平面上的直线三角形A'B'C'相对应时,必有叫平面上的三直线通过w=∞点,即三直线交于w=∞点,因而对应的z平面上的三圆弧必交于一点z=一(如图7—17),这就是必要条件．充分性：如果当w平面上的某三圆弧交于一点z=一时,则三圆周在分式线性函数w=映射下,其像必是过w=∞点的三直线,因而曲线三角形ABC被映射成直线三角形A'B'C'．即w平面上的某三圆周交于一点z=一也是三角形ABC映射成三角形A'B'C'的充分条件．