假设矩阵A和B满足关系式AB＝A＋2B 其中已知且A2－AB＝E 其中E是3阶单位矩阵求矩阵B．

大学本科已帮助：人时间:2024-11-16 11:15:29

假设矩阵A和B满足关系式AB＝A＋2B，其中已知，且A2－AB＝E，其中E是3阶单位矩阵，求矩阵B．
已知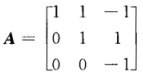
，且A2－AB＝E，其中E是3阶单位矩阵，求矩阵B．
请帮忙给出正确答案和分析，谢谢！

406***102

2024-11-16 11:15:29



正确答案：因｜A｜≠0在A²－AB＝E两边左乘A^－1得 A—B＝A^－1 即 B＝A—A^－1．又由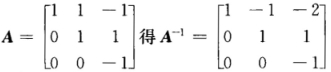从而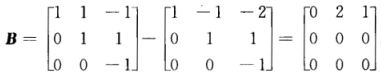
[分析利用A的可逆性将原矩阵方程化简，再求B．[评注解矩阵方程是考研的常见题型，一般利用某些矩阵的可逆性先将已知方程化简，再求解．

判定下列结论是否正确：此题为判断题(对错)。请帮忙给出正确答案和分析谢谢！

判定下列结论是否正确：此题为判断题(对，错)。请帮忙给出正确答案和分析，谢谢！
若｜f(x)｜(x)(x≥α) 则当x>a时必有( )。A．｜f(x)一f(a)｜

若｜f(x)｜(x)(x≥α)，则当x>a时必有( )。A．｜f(x)一f(a)｜<g(x)一g(a)B．｜f(x)一f(a)｜≥g(x)一g(a)C．｜f(x)一f(a)｜=g(x)一g(a)D．｜f(x)-f(a)｜<
设A P均为3阶矩阵 PT为P的转置矩阵且PTAP＝．若P＝(α1 α2 α3) Q＝(α1＋α2

设A，P均为3阶矩阵，PT为P的转置矩阵，且PTAP＝．若P＝(α1，α2，α3)，Q＝(α1＋α2，α2，α3)，则QTAQ为A．B．C．D．请帮忙给出正确答案和分析，谢谢！
某公司每年工资总额在比前年增加20％的基础上再追加200万元若以Wt表示第t年的工资总额(单位：百

某公司每年工资总额在比前年增加20％的基础上再追加200万元，若以Wt表示第t年的工资总额(单位：百万元)，求Wt满足的方程；若2000年该公司的工资总额为1
N(i1i2…in)+N(in…i2i1)=________．请帮忙给出正确答案和分析谢谢！

N(i1i2…in)+N(in…i2i1)=________．请帮忙给出正确答案和分析，谢谢！

判定下列结论是否正确：此题为判断题(对错)。请帮忙给出正确答案和分析谢谢！