9-7 设有一台380V 50HZ 1450r/min 15kW的三角形联结得三相异步电动机 定子
9-7 设有一台380V、50HZ、1450r/min、15kW的三角形联结得三相异步电动机，定子参数与转子参数如折算到同一边时可作为相等,R1=R′2=0.742Ω，每相漏抗为每相电阻的4倍，可取修正系数C1=1+χ1/χm=1.04 ，Rm=9Ω，并且电流增减时漏抗近似为常数。试求：
（1） 在额定运行时的输入功率，电磁功率，内功率以及各项损耗；
（2） 最大电磁转矩，过载能力，以及出现最大转矩时的转差率；
（3） 为了在起动时得到最大转矩，在转子回路中应接入的每相电阻，并用转子电阻的倍数表示之。
参考解答
406***115
2025-02-07 20:43:18
解：（1）
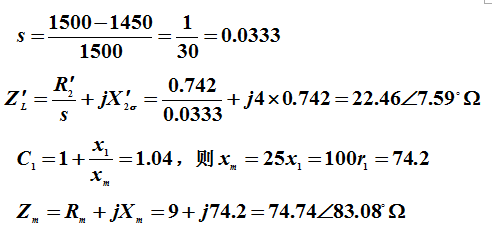
所以 
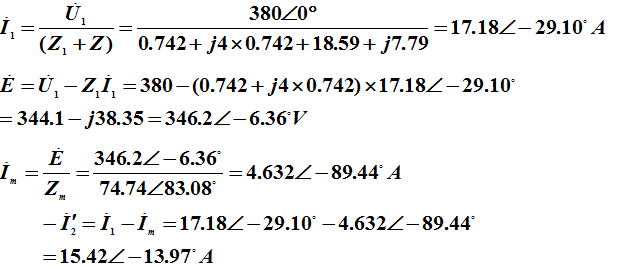
输入功率 
电磁功率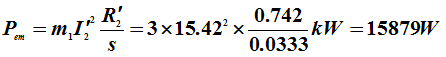 
内功率 
定子铜耗 
转子铜耗 
铁耗
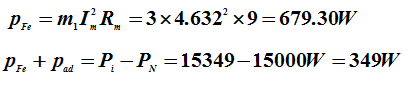
（2）最大转矩
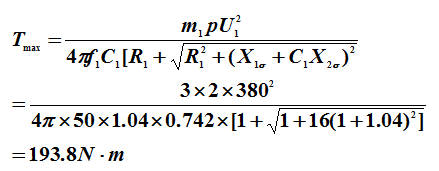
而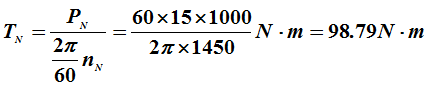 
所以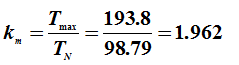 
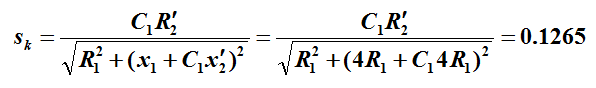
（3）要想起动时得到最大转矩，则应使
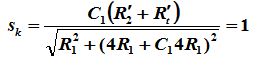
则
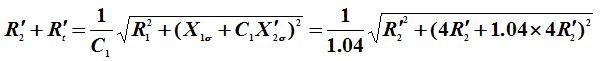
解得 
每相应串入
的电阻方使起动时得到最大转矩。
答案仅供参考，不要直接抄袭哦
相似问题
7-7 三相对称绕组流入三相对称电流试求：（1）当wt=0º时 三相合成磁势基波分量幅值的位置；
7-7 三相对称绕组流入三相对称电流试求：（1）当wt=0º时，三相合成磁势基波分量幅值的位置；（2）wt=120º时，三相合成磁势基波分量幅值的位置；（3）w
高等数学复旦大学出版第三版下册课后习题答案 已知四点A(1 -2 3) B(4 -4 -3)
高等数学复旦大学出版第三版下册课后习题答案 已知四点A(1，-2，3)，B(4，-4，-3)，C(2，4，3)，D(8，6，6)，求向量AB在向量CD上的投影
求下列极限：(1)lim(x→3) (x2－3)／(x2＋1); (2)lim(x→1) (x2＋x
求下列极限：(1)lim(x→3) (x2－3)／(x2＋1); (2)lim(x→1) (x2＋x)／(x4－3x2＋1)求下列极限：
判断下列函数的奇偶性:(1)f(x)=√(1-x)+√(1+x)
判断下列函数的奇偶性:(1)f(x)=√(1-x)+√(1+x)
证明:(1)arcsin hx=ln(x＋√(1＋x2) (2)arctan hx=(1／2)ln(
证明:(1)arcsin hx=ln(x＋√(1＋x2) (2)arctan hx=(1／2)ln(1＋x)／(－x):－1
