证明:(1)arcsin hx=ln(x+√(1+x2) (2)arctan hx=(1/2)ln(
证明:(1)arcsin hx=ln(x+√(1+x2) (2)arctan hx=(1/2)ln(1+x)/(-x):-1 证明:(1)arcsin hx=ln(x+√(1+x2) (2)arctan hx=(1/2)ln(1+x)/(-x):-1<x<1![]()
参考解答
证明:(1)arcsin hx=ln(x+√(1+x2) (2)arctan hx=(1/2)ln(1+x)/(-x):-1<x<1
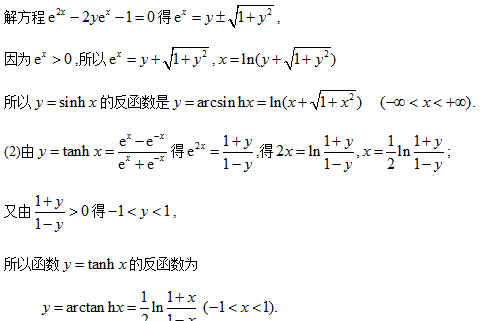
答案仅供参考,不要直接抄袭哦
相似问题
高等数学复旦大学出版第三版下册课后习题答案 设u=a-b+2c v=-a+3b-c.试用a
高等数学复旦大学出版第三版下册课后习题答案 设u=a-b+2c,v=-a+3b-c 试用a, b, c表示2u-3v
设f(x)=2x g(x)=xlnx 求f(g(x)) g(f(x)) f(f(x))和g(g(x)
设f(x)=2x,g(x)=xlnx,求f(g(x)),g(f(x)),f(f(x))和g(g(x))
求下列函数的定义域(1)y=√(4-x)+arctan(1/x)高等数学复旦大学出版第三版上册课后答
求下列函数的定义域(1)y=√(4-x)+arctan(1/x)高等数学复旦大学出版第三版上册课后答案习题一第2题求下列函数的定义域
高等数学复旦大学出版第三版下册课后习题答案第17题 供大家参考学习
高等数学复旦大学出版第三版下册课后习题答案第17题,供大家参考学习
已知两点M1(2 5 -3) M2(3 -2 5) 点M在线段M1M2上 且M1M=3MM2 求向径
已知两点M1(2,5,-3),M2(3,-2,5),点M在线段M1M2上,且M1M=3MM2,求向径OM的坐标 高等数学复旦大学出版第三版下册课后习题答案 已知两点M1(












