现需要设计一个仓库 它由上下两部分组成 上部分的形状是正四棱锥P-A1B1C1D1 下部分的形状是正
现需要设计一个仓库,它由上下两部分组成,上部分的形状是正四棱锥P-A1B1C1D1,下部分的形状是正四棱柱ABCD- A1B1C1D1 (如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的四倍.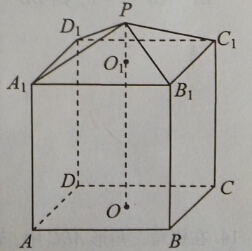
(1) 若AB=6m,PO1=2m,则仓库的容积是多少?
(2) 若正四棱锥的侧棱长为6 m,则当PO1为多少时,仓库的容积最大?
参考解答
正确答案及解析:

相似问题
在锐角三角形ABC中 若sinA=2sinBsinC 则tanAtanBtanC的最小值是_____
在锐角三角形ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是_____
执行右边的程序框图 若输入n的值为3 则输出的S的值为____.
执行右边的程序框图,若输入n的值为3,则输出的S的值为____
△ABC中 角A B C的对边分别是a b c 已知b=c a2=2b2(1-sinA) 则A=(A
△ABC中,角A,B,C的对边分别是a,b,c,已知b=c,a2=2b2(1-sinA),则A=(A)3π 4(B)π 3(C)π 4(D)π 6
已知函数f(x)的定义域为R.当x1/2时 f(x+1/已知函数f(x)的定义域为R.当x
已知函数f(x)的定义域为R 当x1/2时,f(x+1/已知函数f(x)的定义域为R 当x<0时,f(x)=x3-1;当-1≤x≤1时,f(-x)= x="">1 2时,f(x+1 2)=f(x—1 2) 则f(6)=(A)-2(B)-1(C)0(D)2
已知函数f(x)=ax+bx(a>0 b>0 a≠1 b≠1).(1) 设a=2 b=1/2 .①
已知函数f(x)=ax+bx(a>0,b>0,a≠1,b≠1) (1) 设a=2,b=1 2 ① 求方程f(x)=2的根;②若对任意x∈R,不等式f(2x)≥mf(x)-6恒成立,求实数m的最大值;(2)若0












