函数集合V3={α2x2+a1x+a0ex|a2 a1 a0∈R} 对于函数的线性运算构成三维线性空
函数集合V3={α2x2+a1x+a0ex|a2，a1，a0∈R} 对于函数的线性运算构成三维线性空间．在V3中取一个基： α1=x2ex，α2=xex，α3=ex，求微分运算D在这个基下的矩阵．
请帮忙给出正确答案和分析，谢谢！
参考解答
4j8***101
2024-11-11 06:37:23
正确答案：根据微分运算的规则容易看出D是V3中的一个线性变换直接计算基向量在D下的像即可求得D在给定基下的矩阵：D(α1)=D(x2ex)=x2ex+2xex=(α1α2α3)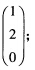
D(α2)=D(xex)=xex+ex=(α1α2α3)
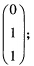D(α3)=D(ex)=ex=(α1α2α3)
于是有 D(α1α2α3)=(α1α2α3)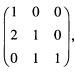
上式等号右端的矩阵就是D在上述基下的矩阵．
根据微分运算的规则,容易看出D是V3中的一个线性变换,直接计算基向量在D下的像,即可求得D在给定基下的矩阵：D(α1)=D(x2ex)=x2ex+2xex=(α1,α2,α3)D(α2)=D(xex)=xex+ex=(α1,α2,α3)D(α3)=D(ex)=ex=(α1,α2,α3)于是有D(α1,α2,α3)=(α1,α2,α3)上式等号右端的矩阵就是D在上述基下的矩阵．
相似问题
设b1=a1+a2 b2=a2+a3 b3=a3+a4 b4=a4+a1 证明向量组b1 b2 b3
设b1=a1+a2，b2=a2+a3，b3=a3+a4，b4=a4+a1，证明向量组b1，b2，b3，b4线性相关．请帮忙给出正确答案和分析，谢谢！
设平面图形A由x2+y2≤2x与y≥x所确定 求图形A绕直线x=2旋转一周所得旋转体的体积．请帮忙给
设平面图形A由x2+y2≤2x与y≥x所确定，求图形A绕直线x=2旋转一周所得旋转体的体积．请帮忙给出正确答案和分析，谢谢！
可以用万能代换求所有三角函数有理式的积分吗?请帮忙给出正确答案和分析 谢谢！
可以用万能代换求所有三角函数有理式的积分吗?请帮忙给出正确答案和分析，谢谢！
已知三阶矩阵A的特征值为1 2 3 求|A3一5A2+7A|．请帮忙给出正确答案和分析 谢谢！
已知三阶矩阵A的特征值为1，2，3，求|A3一5A2+7A|．请帮忙给出正确答案和分析，谢谢！
各种波谱法原理不同 其特点和应用也各不相同。每种波谱法也都有其适用范围和局限性。在使用时应根据___
各种波谱法原理不同，其特点和应用也各不相同。每种波谱法也都有其适用范围和局限性。在使用时应根据_______、_______、_______及_______选择合适的方法
