半径为R的绝缘球体 球上电荷分布不是均匀的 其体电荷密度与半径成正比 即ρ=kr(k>0)．求球内外

正确答案：由于ρ只与r有关与角度无关电荷仍为球对称分布故场强E也呈球对称分布即在与球心等距离的各点处场强E的大小相同方向沿半径方向．因此可用高斯定理求解场强然后再用电势定义式(14-10)求电势分布． (1)求场强E．取半径为r＜R的同心球面为高斯面S₁．由定义通过高斯面的电通量为 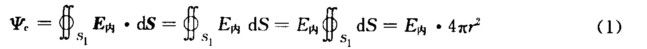由高斯定理得 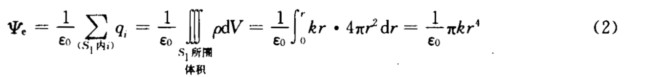由式(1)和(2)解得 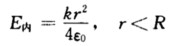同理取半径为r>R的同心球面为高斯面S₂．由定义通过高斯面的电通量为 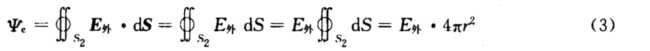由高斯定理得 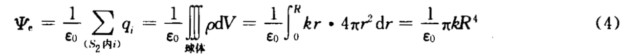由式(3)和(4)解得 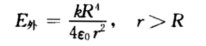(2)求电势U．球外区域r>R选取积分路径沿半径直至无限远．则 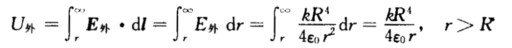球内区域r＜R仍选取积分路径沿半径直至无限远则 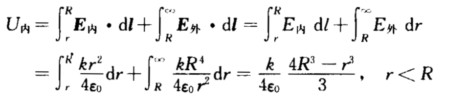场强和电势随半径变化的规律如图14-5所示．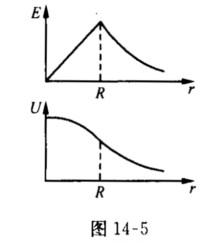
由于ρ只与r有关,与角度无关,电荷仍为球对称分布,故场强E也呈球对称分布,即在与球心等距离的各点处场强E的大小相同,方向沿半径方向．因此,可用高斯定理求解场强,然后再用电势定义式(14-10)求电势分布．(1)求场强E．取半径为r＜R的同心球面为高斯面S1．由定义,通过高斯面的电通量为由高斯定理得由式(1)和(2)解得同理,取半径为r>R的同心球面为高斯面S2．由定义,通过高斯面的电通量为由高斯定理得由式(3)和(4)解得(2)求电势U．球外区域r>R,选取积分路径沿半径直至无限远．则球内区域r＜R,仍选取积分路径沿半径直至无限远,则场强和电势随半径变化的规律如图14-5所示．