参考解答
正确答案:由物理意义可知稳定解为 x=Acos(ωt+φ)代入得 Aω2cos(ωt+φ+π)+2βAωcos(ωt+φ+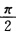 )+ω02Acos(ωt+φ)=hcosωt因为x=Acos(ωt+φ)是解所以上式变为恒等式。令ωt=0得 Aω2cos(φ+π)+2βAcos(φ一
)+ω02Acos(ωt+φ)=hcosωt因为x=Acos(ωt+φ)是解所以上式变为恒等式。令ωt=0得 Aω2cos(φ+π)+2βAcos(φ一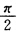 )+ω02Acos(φ)=h (ω02一ω2)Acos9-2βAωsinφ=h
)+ω02Acos(φ)=h (ω02一ω2)Acos9-2βAωsinφ=h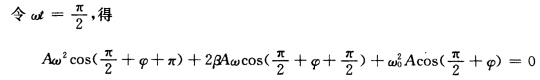 (ω2一ω02)Asinφ一2βAωcosφ=0整理得h2=(2βAω)2+(ω02A一ω2A)2
(ω2一ω02)Asinφ一2βAωcosφ=0整理得h2=(2βAω)2+(ω02A一ω2A)2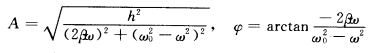 或由sinωtcosωt的非相关性其系数为零可得。
或由sinωtcosωt的非相关性其系数为零可得。
由物理意义可知,稳定解为x=Acos(ωt+φ)代入得Aω2cos(ωt+φ+π)+2βAωcos(ωt+φ+)+ω02Acos(ωt+φ)=hcosωt因为x=Acos(ωt+φ)是解,所以上式变为恒等式。令ωt=0,得Aω2cos(φ+π)+2βAcos(φ一)+ω02Acos(φ)=h(ω02一ω2)Acos9-2βAωsinφ=h(ω2一ω02)Asinφ一2βAωcosφ=0整理得h2=(2βAω)2+(ω02A一ω2A)2或由sinωt,cosωt的非相关性,其系数为零可得。
相似问题
如图2—18所示 均质细杆可在竖直平面内转动 求均质杆与木块完全非弹性碰撞后木块的速度。杆长l 杆的
如图2—18所示,均质细杆可在竖直平面内转动,求均质杆与木块完全非弹性碰撞后木块的速度。杆长l,杆的质量M,木块质量m;木块初始位置与轴连线平行于g。
相邻两波节之间质点振动同相位 任一波节两侧振动反相 在波节处存在相位突变。请帮忙给出正确答案和分析
相邻两波节之间质点振动同相位,任一波节两侧振动反相,在波节处存在相位突变。请帮忙给出正确答案和分析,谢谢!
一个可看成孤立的导体球壳层 内半径为a 带电Q;外半径为b 带电Q 如图4—26所示。求静电能。 请
一个可看成孤立的导体球壳层,内半径为a,带电Q;外半径为b,带电Q,如图4—26所示。求静电能。 请帮忙给出正确答案和分析,谢谢!
一个不带电荷的可看成孤立的导体球壳层 内半径为a 外半径为b 沿径向有一小孔 如图4—25所示。将一
一个不带电荷的可看成孤立的导体球壳层,内半径为a,外半径为b,沿径向有一小孔,如图4—25所示。将一个带电荷为q的点电荷从无穷远处移到球心,则外力所
次品数量。请帮忙给出正确答案和分析 谢谢!
次品数量。请帮忙给出正确答案和分析,谢谢!


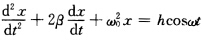 的振幅。
的振幅。









