假设矩阵A和B满足关系式AB＝A＋2B 其中设(2E—C－1B)AT＝C－1 其中E是4阶单位矩阵

大学本科已帮助：人时间:2024-11-16 12:48:35

假设矩阵A和B满足关系式AB＝A＋2B，其中设(2E—C－1B)AT＝C－1，其中E是4阶单位矩阵，AT是4阶矩阵A的转置
设(2E—C－1B)AT＝C－1，其中E是4阶单位矩阵，AT是4阶矩阵A的转置矩阵，
，求A．
请帮忙给出正确答案和分析，谢谢！

490***102

2024-11-16 12:48:35



正确答案：由题设得 C(2E—C^－1B)A^T＝E即(2C—B)A^T＝E．由于2C—B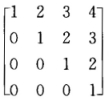＝｜2C—B｜＝1≠0故2C—B可逆．于是 A＝E(2C－B)^－1^T＝[(2c－B)^T^－1
将已知矩阵化简，再利用逆矩阵的性质求A．

假设矩阵A和B满足关系式AB＝A＋2B 其中设n阶矩阵A和B满足条件A＋B＝AB．已知求矩阵A．

假设矩阵A和B满足关系式AB＝A＋2B，其中设n阶矩阵A和B满足条件A＋B＝AB．已知，求矩阵A．设n阶矩阵A和B满足条件A＋B＝AB．已知，求矩阵A．请帮忙给出
设A B为n阶矩阵 A* B*分别是A B对应的伴随矩阵分块矩阵则C的伴随矩阵C*等于A．B．C

设A,B为n阶矩阵，A*，B*分别是A，B对应的伴随矩阵，分块矩阵，则C的伴随矩阵C*等于A．B．C．D．请帮忙给出正确答案和分析，谢谢！
设f(x)=xsinx 则f(100)=(0)=( )．A．50B．一50C．100D．一100请帮

设f(x)=xsinx，则f(100)=(0)=( )．A．50B．一50C．100D．一100请帮忙给出正确答案和分析，谢谢！
利用下列级数设f(x)＝xln(1－x2) (1)将f(x)展开成x的幂级数并求收敛域；(2)利用

利用下列级数设f(x)＝xln(1－x2)，(1)将f(x)展开成x的幂级数，并求收敛域；(2)利用展开式计算f(101)(0设f(x)＝xln(1－x2)，(1)将f(x)展开成x的幂级数，并
300K时 4．0g.dm-3的聚氯乙烯溶液其渗透压为65Pa。试计算聚氯乙烯的平均相对分子质量。

300K时，4．0g dm-3的聚氯乙烯溶液，其渗透压为65Pa。试计算聚氯乙烯的平均相对分子质量。请帮忙给出正确答案和分析，谢谢！

假设矩阵A和B满足关系式AB＝A＋2B 其中设n阶矩阵A和B满足条件A＋B＝AB．已知求矩阵A．