求下列复数域上矩阵的全部特征值和特征向量：请帮忙给出正确答案和分析 谢谢！
求下列复数域上矩阵的全部特征值和特征向量：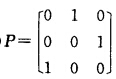
请帮忙给出正确答案和分析，谢谢！
参考解答
481***101
2024-11-13 21:29:41
正确答案：×
可得λ=这就是复数域上P的全部特征值．对于λ=1,求得(1×I-P)X=0的一个基础解系为所以P的属于1的全部特征向量为{k1α1｜k1∈C,且k1≠0)．同理可求得P属于的全部特征向量为{k2α2｜k2∈C,且k2≠0其中P属于的全部特征向量为{k3α3｜k3∈C且k3≠0)其中
相似问题
设A为n阶可逆方阵 α与β均为n维列向量．证明：｜ A+αβT｜=｜A｜(1+βTA-1α)．请帮忙
设A为n阶可逆方阵，α与β均为n维列向量．证明：｜ A+αβT｜=｜A｜(1+βTA-1α)．请帮忙给出正确答案和分析，谢谢！
求解矩阵X请帮忙给出正确答案和分析 谢谢！
求解矩阵X请帮忙给出正确答案和分析，谢谢！
证明：对于任一s×n矩阵A 都有AA AA是对称矩阵．请帮忙给出正确答案和分析 谢谢！
证明：对于任一s×n矩阵A，都有AA，AA是对称矩阵．请帮忙给出正确答案和分析，谢谢！
设rn的下述子集W是一个子空间：W={(α1 α2 … αr 0 … 0)｜αi∈K i=1 2 …
设rn的下述子集W是一个子空间：W={(α1，α2，…，αr，0，…，0)｜αi∈K，i=1，2，…，r)．请帮忙给出正确答案和分析，谢谢！
设A是数域K上s×n矩阵．证明：如果A列满秩 则对于K上任意一个m×n矩阵H 矩阵方程XA=H都有解
设A是数域K上s×n矩阵．证明：如果A列满秩，则对于K上任意一个m×n矩阵H，矩阵方程XA=H都有解，并且找出它的一些解．请帮忙给出正确答案和分析，谢谢！
