设P是酉矩阵 A=diag(a1 a2 … an) 证明PA的特征值μ满足不等式m≤∣μ∣≤M 其中
设P是酉矩阵，A=diag(a1，a2，…，an)，证明PA的特征值μ满足不等式m≤∣μ∣≤M，其中m=min∣ai∣，M=max∣ai∣．
请帮忙给出正确答案和分析，谢谢！
参考解答
481***101
2024-11-12 00:21:07
正确答案：因为P是酉矩阵所以PHP=E又因为(PA)H(PA)=AHPHPA=AHA所以由Browne定理知PA的特征值μ满足不等式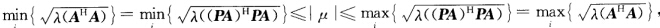
而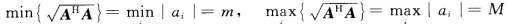
所以m≤∣μ∣≤M．
因为P是酉矩阵,所以PHP=E,又因为(PA)H(PA)=AHPHPA=AHA,所以由Browne定理知,PA的特征值μ满足不等式,而,所以m≤∣μ∣≤M．
相似问题
证明：(A+)+=A．请帮忙给出正确答案和分析 谢谢！
证明：(A+)+=A．请帮忙给出正确答案和分析，谢谢！
讨论下列幂级数的敛散性： (1)； (2)请帮忙给出正确答案和分析 谢谢！
讨论下列幂级数的敛散性： (1)； (2)请帮忙给出正确答案和分析，谢谢！
设A B∈Cn×n AB=BA 证明： sin(A+B)=sin Acos B+cos Asin B
设A，B∈Cn×n，AB=BA，证明： sin(A+B)=sin Acos B+cos Asin B，cos(A+B)=cos Acos B－sin Asin B．请帮忙给出正确答案和分析，谢谢！
求矩阵A=的奇异值分解．请帮忙给出正确答案和分析 谢谢！
求矩阵A=的奇异值分解．请帮忙给出正确答案和分析，谢谢！
若∥.∥是算子范数 则 (1)∥E∥=1； (2)∥A－1∥≥∥A∥－1； (3)请帮忙给出正确答案
若∥ ∥是算子范数，则 (1)∥E∥=1； (2)∥A－1∥≥∥A∥－1； (3)请帮忙给出正确答案和分析，谢谢！
