设f(x)在(－1 1)内具有二阶连续导数且f'(x)≠0 试证： (1)对于(－1 1)内的任一x
设f(x)在(－1，1)内具有二阶连续导数且f"(x)≠0，试证： (1)对于(－1，1)内的任一x≠0，存在唯一的θ(x)∈(0，1)，使f(x)＝f(0)＋xf(θ(x)x)成立； (2)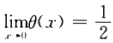
．
请帮忙给出正确答案和分析，谢谢！
参考解答
481***101
2024-11-09 23:01:07
正确答案：(1)直接用拉格朗日中值定理即可得存在性用单调性判断唯一性；(2)由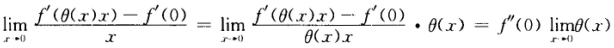
可得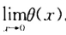
也可用f(x)二阶泰勒展开式并与(1)中已有的结果进行对比推导．
(1)直接用拉格朗日中值定理即可得存在性,用单调性判断唯一性；(2)由,可得,也可用f(x)二阶泰勒展开式,并与(1)中已有的结果进行对比推导．
相似问题
求由下列方程所确定的隐函数y＝y(x)的导数dy／dx： (1)y＝1－xey； (2)xy＝ex＋
求由下列方程所确定的隐函数y＝y(x)的导数dy／dx： (1)y＝1－xey； (2)xy＝ex＋y； (3)xy＝yx； (4)y＝1＋xsiny．请帮忙给出正确答案和分析，谢谢！
设函数f(x)＝(x2－3x＋2)sinx 则方程fˊ(x)＝0在(0 π)内根的个数为( )。A．
设函数f(x)＝(x2－3x＋2)sinx，则方程fˊ(x)＝0在(0，π)内根的个数为( )。A．0个B．至多1个C．2个D．至少3个请帮忙给出正确答案和分析，谢谢！
利用带有佩亚诺型余项的麦克劳林公式求下列极限： 请帮忙给出正确答案和分析 谢谢！
利用带有佩亚诺型余项的麦克劳林公式求下列极限： 请帮忙给出正确答案和分析，谢谢！
求曲线y＝cosx上点(π／3 1／2)处的切线方程和法线方程．请帮忙给出正确答案和分析 谢谢！
求曲线y＝cosx上点(π／3，1／2)处的切线方程和法线方程．请帮忙给出正确答案和分析，谢谢！
求导数： 请帮忙给出正确答案和分析 谢谢！
求导数： 请帮忙给出正确答案和分析，谢谢！
