验证下列函数满足波动方程utt＝a2uxx： (1)u＝sin(kx)sin(akt)； (2)u＝

正确答案：(1)u_x＝kcos(kx)sin(akt) u_xx＝－k²sin(kx)sin(akt) u_t＝aksin(kx)cos(akt)u_tt＝－a²k²sin(kx)sin(akt)综上u_tt＝a²u_xx成立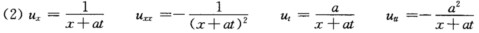；综上u_tt＝a²uu_xx成立；(3)u_x＝cos(x－at)u_xx＝－asin(x－at) u_t＝－acos(x－at) u_tt＝a²sin(x－at)综上u_tt＝a²u_xx成立．
(1)ux＝kcos(kx)sin(akt)uxx＝－k2sin(kx)sin(akt)ut＝aksin(kx)cos(akt)utt＝－a2k2sin(kx)sin(akt)综上,utt＝a2uxx成立；综上,utt＝a2uuxx成立；(3)ux＝cos(x－at)uxx＝－asin(x－at)ut＝－acos(x－at)utt＝a2sin(x－at)综上,utt＝a2uxx成立．