求下列矩阵的最大秩分解式. (1)A= (2)A=请帮忙给出正确答案和分析 谢谢!
求下列矩阵的最大秩分解式. (1)A= , (2)A=
, (2)A=
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)对矩阵A实行行初等变换得 取B=
取B=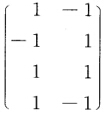 D=
D=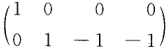 则A=BD就是矩阵A的最大秩分解. (2)同理对矩阵A进行行初等变换可得
则A=BD就是矩阵A的最大秩分解. (2)同理对矩阵A进行行初等变换可得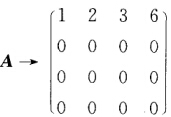 取B=
取B=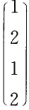 D=(1 2 3 6)则A=BD就是矩阵A的最大秩分解.
D=(1 2 3 6)则A=BD就是矩阵A的最大秩分解.
(1)对矩阵A实行行初等变换,得取B=,D=,则A=BD就是矩阵A的最大秩分解.(2)同理对矩阵A进行行初等变换,可得取B=,D=(1236),则A=BD就是矩阵A的最大秩分解.
相似问题
设Α和B分别是n×S和S×P矩阵.n维行向量X满足XΑB=0.令V={Y|Y=XΑ XΑB=0).求
设Α和B分别是n×S和S×P矩阵.n维行向量X满足XΑB=0.令V={Y|Y=XΑ,XΑB=0).求证V是一个线性空间,且dim V=rank(Α)-rank(ΑB).请帮忙给出正确答案和分析,谢谢!
设A=AH 证明:(A2)+=(AH)2 AA+=A+A A+A2=A2A+ A2(A2)+=(A2
设A=AH,证明:(A2)+=(AH)2,AA+=A+A,A+A2=A2A+,A2(A2)+=(A2)+A2=AA+.请帮忙给出正确答案和分析,谢谢!
设A=(αij)∈Cn×n可逆 λ为特征值 则∥A-1∥2-1≤∣λ∣≤∥A∥2.请帮忙给出正确答案
设A=(αij)∈Cn×n可逆,λ为特征值,则∥A-1∥2-1≤∣λ∣≤∥A∥2.请帮忙给出正确答案和分析,谢谢!
设A∈Cm×n rank(A)=γ 若有m阶可逆矩阵P和n阶置换矩阵Q 使得 S∈C(n-γ)(m-
设A∈Cm×n,rank(A)=γ,若有m阶可逆矩阵P和n阶置换矩阵Q,使得,S∈C(n-γ)(m-γ).试证:对任给L∈C(n-γ)(m-γ),矩阵是A的一个广义逆,若L=0,
用圆盘定理估计矩阵的特征值和A的谱半径 然后选取一组正数p1 p2 p3对A的特征值作更细的估计.请
用圆盘定理估计矩阵的特征值和A的谱半径,然后选取一组正数p1,p2,p3对A的特征值作更细的估计.请帮忙给出正确答案和分析,谢谢!












