设A为正定Hermite矩阵 B为反Hermite矩阵.试证明:AB与BA的特征值实部为零. (2)
设A为正定Hermite矩阵,B为反Hermite矩阵.试证明:AB与BA的特征值实部为零. (2)设A是n(n>1)阶正定矩阵.α是非零列向量,且α∈Rn.令B=AααT,求B的最大特征值以及B的属于这个特征值的特征子空间的维数和一个基.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)首先注意到AB与BA有着相同的非零特征值因此我们只需证明它们中的任意一个成立即可.不妨设λ为AB的任意一个特征值于是∣λE-AB∣=0.由于A为正定Hermite矩阵所以存在可逆矩阵Q使得A=QHQ将此式代入∣λE一AB∣=0可得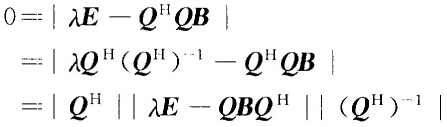 从而有∣AE-QBQH∣=0这表明λ也是QBQH的特征值.注意到QBQH是一个反Hermite矩阵而反Hermite矩阵的特征值为零或纯虚数所以λ为零或纯虚数. (2)由于A正定α≠0可得λ=αTAα>0Aα≠0rank(B)-rank(αT)=1由rank(B)=1知方程组BX=0解空间W0的维数为n—1W0同时也是B的属于特征值0的特征子空间. 由λ>0Aα≠0和BAα=AααTAα=(αTAα)Aα=λAα知λ是B的特征值Aα是B的属于特征值λ的特征向量.设B的属于这个特征值的特征子空间为Wλ由λ≠0Wλ∩W0={0所以dimWλ+dimW0=dim(Wλ+W0)≤n.即dim Wλ≤1而Aα≠0Aα∈WλdimWλ=1Wλ的一组基为Aα且dim Wλ=1=>dimWλ+dimW0=n因此λ=αTAα>0是B的唯一非零特征值也是B的最大特征值.
从而有∣AE-QBQH∣=0这表明λ也是QBQH的特征值.注意到QBQH是一个反Hermite矩阵而反Hermite矩阵的特征值为零或纯虚数所以λ为零或纯虚数. (2)由于A正定α≠0可得λ=αTAα>0Aα≠0rank(B)-rank(αT)=1由rank(B)=1知方程组BX=0解空间W0的维数为n—1W0同时也是B的属于特征值0的特征子空间. 由λ>0Aα≠0和BAα=AααTAα=(αTAα)Aα=λAα知λ是B的特征值Aα是B的属于特征值λ的特征向量.设B的属于这个特征值的特征子空间为Wλ由λ≠0Wλ∩W0={0所以dimWλ+dimW0=dim(Wλ+W0)≤n.即dim Wλ≤1而Aα≠0Aα∈WλdimWλ=1Wλ的一组基为Aα且dim Wλ=1=>dimWλ+dimW0=n因此λ=αTAα>0是B的唯一非零特征值也是B的最大特征值.
(1)首先,注意到AB与BA有着相同的非零特征值,因此我们只需证明它们中的任意一个成立即可.不妨设λ为AB的任意一个特征值,于是∣λE-AB∣=0.由于A为正定Hermite矩阵,所以存在可逆矩阵Q,使得A=QHQ,将此式代入∣λE一AB∣=0可得从而有∣AE-QBQH∣=0,这表明λ也是QBQH的特征值.注意到QBQH是一个反Hermite矩阵,而反Hermite矩阵的特征值为零或纯虚数,所以λ为零或纯虚数.(2)由于A正定,α≠0,可得λ=αTAα>0,Aα≠0,rank(B)-rank(αT)=1,由rank(B)=1,知方程组BX=0解空间W0的维数为n—1,W0同时也是B的属于特征值0的特征子空间.由λ>0,Aα≠0和BAα=AααTAα=(αTAα)Aα=λAα,知λ是B的特征值,Aα是B的属于特征值λ的特征向量.设B的属于这个特征值的特征子空间为Wλ,由λ≠0,Wλ∩W0={0,所以dimWλ+dimW0=dim(Wλ+W0)≤n.即dimWλ≤1,而Aα≠0,Aα∈Wλ,dimWλ=1,Wλ的一组基为Aα,且dimWλ=1=>dimWλ+dimW0=n,因此,λ=αTAα>0是B的唯一非零特征值,也是B的最大特征值.
相似问题
设A B都是实对称矩阵 A的一切特征值在区间[a b]上 B的一切特征值在区间 [c d]上.证明:
设A,B都是实对称矩阵,A的一切特征值在区间[a,b]上,B的一切特征值在区间 [c,d]上.证明:A+B的特征值必在区间[a+c,b+d]上.请帮忙给出正确答案和分析,谢谢!
设PE∈Cm×m Q∈Cn×n均为可逆矩阵 且有B=PAQ 证明:Q-1A-P-1∈B{1}.请帮忙
设PE∈Cm×m,Q∈Cn×n均为可逆矩阵,且有B=PAQ,证明:Q-1A-P-1∈B{1}.请帮忙给出正确答案和分析,谢谢!
用Schmidt正交化方法求矩阵A的分解 其中请帮忙给出正确答案和分析 谢谢!
用Schmidt正交化方法求矩阵A的分解,其中请帮忙给出正确答案和分析,谢谢!
试证:对于每一个实对称矩阵A 都存在一个n阶方阵S 使A=S3.请帮忙给出正确答案和分析 谢谢!
试证:对于每一个实对称矩阵A,都存在一个n阶方阵S,使A=S3.请帮忙给出正确答案和分析,谢谢!
设A∈Cm×m和B∈Cn×n均可逆 证明: (1)若D∈Cm×n是左可逆的 则ADB是左可逆的; (
设A∈Cm×m和B∈Cn×n均可逆,证明: (1)若D∈Cm×n是左可逆的,则ADB是左可逆的; (2)若D∈Cm×n是右可逆的,则ADB是右可逆的.请帮忙给出正确答案和分析,谢谢!












