如果f'(x)在[a b]上连续 在（a b）内可导且f’(a) ≥0 f”(x)>0 证明：f(b
如果f"(x)在[a，b]上连续，在（a，b）内可导且f’(a) ≥0,f”(x)>0,证明：f(b)>f(a).
如果f'(x)在[a，b]上连续，在（a，b）内可导且
证明：f(b)>f(a).
参考解答
473***115
2025-02-06 09:07:21
如果f'(x)在[a，b上连续，在（a，b）内可导且f’(a) ≥0,f”(x)>0,证明：f(b)>f(a).
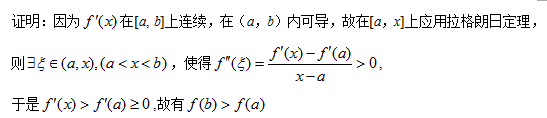
答案仅供参考，不要直接抄袭哦
相似问题
试证:方程sin x=x只有一个实根.试证:方程只有一个实根.
试证:方程sin x=x只有一个实根 试证:方程只有一个实根
高等数学复旦大学出版第三版下册课后习题答案习题十 试讨论下列无界函数的二重积分的收敛性：
高等数学复旦大学出版第三版下册课后习题答案习题十 试讨论下列无界函数的二重积分的收敛性：
一个水槽长12m 横截面是等边三角形 其边长为2m 水以3m3·min-1的速度注入水槽内 当水深
一个水槽长12m，横截面是等边三角形，其边长为2m，水以3m3·min-1的速度注入水槽内，当水深0 5m时，水面高度上升多快？
高等数学复旦大学出版第三版下册课后习题答案习题十 计算积分∫dy∫e-(x2+y2)cos(x
高等数学复旦大学出版第三版下册课后习题答案习题十 计算积分∫dy∫e-(x2+y2)cos(x^2+y^2)dx
高等数学复旦大学出版第三版下册课后习题答案习题九 设空间有n个点 坐标为(xi yi zi)(
高等数学复旦大学出版第三版下册课后习题答案习题九 设空间有n个点，坐标为(xi,yi,zi)(i=1,2, ,n) ,试在xOy面上找一点，使此点与这n个点的距离的平方和最小。
