有一个与轻弹簧相连的小球 沿X轴做简谐振动 其表达式用余弦函数表示 振幅为A．若t=0时小球的状态为

正确答案：法一 (1)初始条件为x₀=-Av₀=0．将初始条件代入运动学方程x=Acos(ωt+φ)有Acosφ=-A即cosφ=-1．于是有 φ=πrad此初相同时满足v₀=-ωAsinπ=0．因此初相即为φ=π． (2)初始条件为x₀=0v₀＜0时．将初始条件代入运动学方程有Acosφ=0即cosφ=0．解得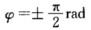考虑到v₀=-ωAsinφ＜0即sinφ＞0．因此初相取φ=π/2． (3)初始条件为x₀=A/2v₀＞0．解法同上可得到 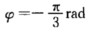法二 旋转矢量法．(1)矢量A位于如图6-1(a)所示的位置表示t=0时x₀=-A小球正处于负向最大位移处φ=π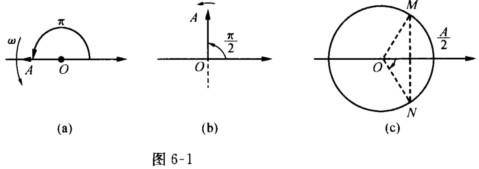． (2)如图6-1(b)所示矢量A位于所示位置时矢端在X轴上的投影为零．又因为矢量A逆时针旋转所以A的位置就表示t=0时小球位移x₀=0且沿x轴负方向运动所以φ=π/2． (3)如图6-1(c)因x₀=A/2矢量的端点应在以O为圆心、以｜A｜为半径的圆周上且与过x=A/2并垂直于X轴的直线交于点M或N．义因为小球向正方向运动所以A应位于ON处即φ=-(π/3) 法三 根据φ=arctan(-v₀/ωx₀)求解此题．(1)φ=arctan(0/-ωA)=π(2)φ=arctan(∞)=π/2．(3)因未给出v₀的数值故不能用此法求出初相φ.
以上求初相的三种方法中，第一种方法物理意义明确；第二种方法直观而简捷；使用第三种方法时，可以把公式tanφ=-v0/ωx0的负号放在分子上?这样，分子部分的符号对应着sinφ的符号，而分母的符号对应着cosφ的符号．这样就可以帮助我们最后确定φ的值．如(1)φ=arctanx，φ可取0或π，但因为-ωA＜0，故φ=π．但若只给出初始时刻的位移和运动方向，而没给出v0的具体数值时，用法三也无法解得φ的数值，如本题(3)的情况．