将焦距f=20 cm的薄凸透镜沿正中切去宽度为α的一部分 如图(a)所示 再把余下的两部分粘合起来
将焦距f=20 cm的薄凸透镜沿正中切去宽度为α的一部分,如图(a)所示,再把余下的两部分粘合起来,构成一粘合透镜。如图中,D=2 cm,在粘合透镜的中心轴上的一侧距透镜20 cm处,置一波长λ=500 nm的单色点光源P;在透镜的另一侧,置一垂直于中心轴线的屏.屏上观察到的干涉条纹的间距为△y=0.2 mm。 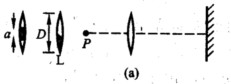 试求:(1)切去部分的宽度α为多少? (2)为获得最多的干涉条纹,屏应离透镜多远?
试求:(1)切去部分的宽度α为多少? (2)为获得最多的干涉条纹,屏应离透镜多远?
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:×
解:(1)首先探讨粘合透镜的上半部分的成像。如图(b)所示,粘合透镜的中心轴线为OO,实线表示上半透镜,虚线表示的是未切割前整个透镜的其余部分,整块透镜的光轴为O'O'。半块透镜的成像规律与完整的透镜相同。这里,物点P置于粘合透镜的中心轴线上,即在透镜的光轴上方α/2处,离开透镜光心的水平距离恰好为透镜的焦距,那么,处于焦平面上的物点P发出的光线,经透镜折射后成为一束向一方倾斜的平行光束,它与O'O'的夹角为θ/2,其值近似为(α/2)/f',当透镜完整时,光束的宽度为(透镜的直径)×cos(θ/2)≈透镜的直径由于θ很小,故对于上半块透镜,光束的宽度为D/2。同理,P点发出的光线,经下半块透镜折射后,形成向上偏折的平行光束.根据对称性,它与O'O'轴成θ/2,宽度也为D/2。在透镜的右方,成为夹角为θ的两束平行光的干涉,如图(c)的斜线所示为干涉区可知干涉条纹的间距△y满足2△ysin(θ/2)=λ在θ很小的条件下,上式变为△yθ=λ(2)综上所述,干涉条纹的间距△y与屏离开透镜L的距离无关,这正是在两束平行光干涉的特定条件下成立,附带应申明的是屏应位于两束光的相干叠加区中才能观察到干涉条纹。由于条纹是等距的,显而易见,如图(e)所示,屏位于GH处可取得最多的干涉条纹。GH平面到透镜L的距离为
相似问题
以白光正入射在一光栅上 将在衍射角为30°方向上观察到600 nm的第二级主最大 若能在该处分辨△λ
以白光正入射在一光栅上,将在衍射角为30°方向上观察到600 nm的第二级主最大,若能在该处分辨△λ=0.005 nm的两条光谱线,可是在30°衍射方向却难以
为测定波片的相位延迟角δ 采用图10-11a所示的实验装置:使一束自然光相继通过起偏器 待测波片 λ
为测定波片的相位延迟角δ,采用图10-11a所示的实验装置:使一束自然光相继通过起偏器、待测波片、λ/4片和检偏器。当起偏器的透光轴和λ/4片的快轴设
已知物镜直径为D 眼睛瞳孔的直径为d 为了充分利用望远镜的分辨率 其放大率应为( )。请帮忙给出正确
已知物镜直径为D,眼睛瞳孔的直径为d,为了充分利用望远镜的分辨率,其放大率应为( )。请帮忙给出正确答案和分析,谢谢!
折射率分别为n1和n2的两种液体 其中n2>n1 它们被光栅常数为d的平面透射光栅所隔开。今有一在液
折射率分别为n1和n2的两种液体,其中n2>n1,它们被光栅常数为d的平面透射光栅所隔开。今有一在液体n1中波长为λ的单色平行光以入射角θ照亮了光栅的N个缝
用负单轴晶体制成的波片 其快轴A.平行于光轴。B.垂直于光轴。C.平行于波片表面。D.垂直于入射平面
用负单轴晶体制成的波片,其快轴A.平行于光轴。B.垂直于光轴。C.平行于波片表面。D.垂直于入射平面。此题为多项选择题。请帮忙给出正确答案和分析,谢谢!












