设A为n阶实对称矩阵 且A3一3A2+5A一3E=O证明：A正定。请帮忙给出正确答案和分析 谢谢！
设A为n阶实对称矩阵，且A3一3A2+5A一3E=O证明：A正定。
请帮忙给出正确答案和分析，谢谢！
参考解答
463***101
2024-11-13 14:53:37
正确答案：设λ是A的任一特征值对应特征向量为x≠0即Ax=λx则有(A3一3A2一5A一3E)x=(λ3一3λ2+5λ一3)x=0所以λ应满足λ3一3λ2一5λ一3=(λ一1)(λ2一2λ+3)=0解得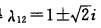
或λ3=1因为A为实对称矩阵故其特征值只有实数λ=1即A的全部特征值都大于零所以A为正定矩阵。
设λ是A的任一特征值,对应特征向量为x≠0,即Ax=λx,则有(A3一3A2一5A一3E)x=(λ3一3λ2+5λ一3)x=0,所以λ应满足λ3一3λ2一5λ一3=(λ一1)(λ2一2λ+3)=0,解得或λ3=1因为A为实对称矩阵,故其特征值只有实数λ=1,即A的全部特征值都大于零,所以A为正定矩阵。
相似问题
有A B C三个事件： (1)若B发生 A不发生 则这个事件可表示为________； (2)若A
有A，B，C三个事件： (1)若B发生，A不发生，则这个事件可表示为________； (2)若A，B，C至少有一个发生，则这个事件可表示为________； (3)若A，B，C
函数f(x)＝ln cos(3x＋1)的复合过程是( )．A．y＝lnu u＝cosv v＝3x＋1
函数f(x)＝ln cos(3x＋1)的复合过程是( )．A．y＝lnu，u＝cosv，v＝3x＋1B．y＝u，u＝ln cosv，v＝3x＋1C．y＝lnu，u＝cos(3x＋1)D．y＝lnu，u＝v，v
已知函数y＝xex 则y'＝_______．请帮忙给出正确答案和分析 谢谢！
已知函数y＝xex，则y "＝_______．请帮忙给出正确答案和分析，谢谢！
当拉格朗日中值定理中 f(x)满足_________时 即为罗尔定理．请帮忙给出正确答案和分析 谢谢
当拉格朗日中值定理中，f(x)满足_________时，即为罗尔定理．请帮忙给出正确答案和分析，谢谢！
在给定显著性水平a＝0．02时 若原假设被拒绝 则认为( )．A．原假设一定不正确B．原假设正确的概
在给定显著性水平a＝0．02时，若原假设被拒绝，则认为( )．A．原假设一定不正确B．原假设正确的概率不会超过0．02C．原假设正确是小概率事件D．原假设不
