求一仿射变换 它使直线χ+2y-1=0上的每个点都不变 且使点(1 -1)变为点(-1 2).请帮忙
求一仿射变换,它使直线χ+2y-1=0上的每个点都不变,且使点(1,-1)变为点(-1,2).
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:在直线χ+2y-1=0上任取两点A(10)B(-11)由于A(10)→A(10)B(-11)→B(-11)又点(1-1)→(-12)此三点不共线从而可惟一确定一个仿射变换将它们的坐标代入仿射变换式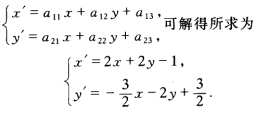
在直线χ+2y-1=0上任取两点A(1,0),B(-1,1),由于A(1,0)→A(1,0),B(-1,1)→B(-1,1),又点(1,-1)→(-1,2),此三点不共线,从而可惟一确定一个仿射变换,将它们的坐标代入仿射变换式
相似问题
平行且相等的二线段的仿射对应图形是:A.相等且相交的二线段;B.一线段;C.不等的平行线段;D.相等
平行且相等的二线段的仿射对应图形是:A.相等且相交的二线段;B.一线段;C.不等的平行线段;D.相等的平行线段.请帮忙给出正确答案和分析,谢谢!
设区域D是由y=x-1 y=x+1 x=2及坐标轴围成的区域(图3-1) (X Y)服从区域D上的均
设区域D是由y=x-1,y=x+1,x=2及坐标轴围成的区域(图3-1),(X,Y)服从区域D上的均匀分布. (1)求(X,Y)的密度函数;(2)求X,Y的边缘密度函数.请帮忙
设(X Y)是二维离散型随机向量 其分布为P(X=xi Y=yj}=pij(i=1 2 … m;j=
设(X,Y)是二维离散型随机向量,其分布为P(X=xi,Y=yj}=pij(i=1,2,…,m;j=1,2,…,n),称(pij)m×n为联合概率矩阵.证明:X与Y相互独立的充要条件
已知X服从[0 1]上的均匀分布 Y~N(0 1) 且X与Y相互独立 求(X Y)的密度函数.请帮忙
已知X服从[0,1]上的均匀分布,Y~N(0,1),且X与Y相互独立,求(X,Y)的密度函数.请帮忙给出正确答案和分析,谢谢!
关于点对称的图形的仿射对应图形是:A.关于点对称的图形;B.不一定关于点对称的图形.请帮忙给出正确答
关于点对称的图形的仿射对应图形是:A.关于点对称的图形;B.不一定关于点对称的图形.请帮忙给出正确答案和分析,谢谢!












