某工厂有A B C三台机器 可加工Ⅰ Ⅱ Ⅲ三种零件 它们在一天内的效率表如表3.5所示。 如果加
某工厂有A,B,C三台机器,可加工Ⅰ,Ⅱ,Ⅲ三种零件,它们在一天内的效率表如表3.5所示。 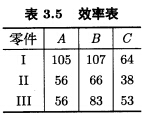 如果加工的零件只要数量相等就能成套,问如何分配机器的加工任务,使得在一天之内能生产出最多的套数?
如果加工的零件只要数量相等就能成套,问如何分配机器的加工任务,使得在一天之内能生产出最多的套数?
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:如果令ABC三台机器都生产第1种零件则105+107+64=276(个)那么A机器所占份额为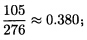 B机器所占份额为
B机器所占份额为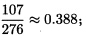 C机器所占份额为
C机器所占份额为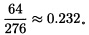 对第ⅡⅢ种零件用上面的方法得表3.6。
对第ⅡⅢ种零件用上面的方法得表3.6。 0次近似的方法:对照各机器找出所占份额的最大数在下面划一横线所对应位置均填上1乘以效率表中对应位置的效率值其他为0就得到了0次近似。在0次近似分配中第11种零件没有机器进行生产因此要重新进行分配。在表3.6中在第二行中的0.413与第二列中的最大数0.432最接近我们把这个比值表的第二行都乘上
0次近似的方法:对照各机器找出所占份额的最大数在下面划一横线所对应位置均填上1乘以效率表中对应位置的效率值其他为0就得到了0次近似。在0次近似分配中第11种零件没有机器进行生产因此要重新进行分配。在表3.6中在第二行中的0.413与第二列中的最大数0.432最接近我们把这个比值表的第二行都乘上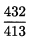 使0.413变为0.432值得表3.7的左边部分:
使0.413变为0.432值得表3.7的左边部分: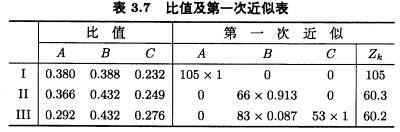 设B机器生产第Ⅱ中零件用的时间为x则生产第Ⅲ种零件所用时间为1一x由成套要求知:66x=83(1一x)+53;x=0.913. 1一x=0.087从而得到表3.7中第一次近似分配方案但第1种零件生产多了还应该进一步调整。表3.7中比值部分第一列最大数0.380最接近第一列中第二行的数0.366因此第一行乘以
设B机器生产第Ⅱ中零件用的时间为x则生产第Ⅲ种零件所用时间为1一x由成套要求知:66x=83(1一x)+53;x=0.913. 1一x=0.087从而得到表3.7中第一次近似分配方案但第1种零件生产多了还应该进一步调整。表3.7中比值部分第一列最大数0.380最接近第一列中第二行的数0.366因此第一行乘以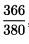 得到表3.8左边部分的比值:
得到表3.8左边部分的比值: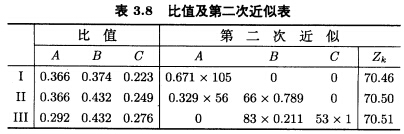 设机器A生产第1种零件的时间为x则生产第Ⅱ种零件的时间为1一x;设机器B生产第Ⅱ种零件的时间为y则生产第Ⅲ种零件的时间为1一y。由成套要求得:105x=56(1一x)+66y=83(1一y)+53整理得:
设机器A生产第1种零件的时间为x则生产第Ⅱ种零件的时间为1一x;设机器B生产第Ⅱ种零件的时间为y则生产第Ⅲ种零件的时间为1一y。由成套要求得:105x=56(1一x)+66y=83(1一y)+53整理得: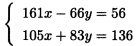 解得:
解得: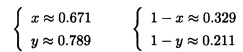 得到表3.8中第二次近似表。三台机器共加工出约70套产品。
得到表3.8中第二次近似表。三台机器共加工出约70套产品。
如果令A,B,C三台机器都生产第1种零件,则105+107+64=276(个)那么,A机器所占份额为B机器所占份额为C机器所占份额为对第Ⅱ,Ⅲ种零件用上面的方法,得表3.6。0次近似的方法:对照各机器找出所占份额的最大数,在下面划一横线,所对应位置均填上1乘以效率表中对应位置的效率值,其他为0,就得到了0次近似。在0次近似分配中,第11种零件没有机器进行生产,因此要重新进行分配。在表3.6中,在第二行中的0.413与第二列中的最大数0.432最接近,我们把这个比值表的第二行都乘上使0.413变为0.432值,得表3.7的左边部分:设B机器生产第Ⅱ中零件用的时间为x,则生产第Ⅲ种零件所用时间为1一x,由成套要求知:66x=83(1一x)+53;x=0.913.1一x=0.087从而得到表3.7中第一次近似分配方案,但第1种零件生产多了,还应该进一步调整。表3.7中比值部分,第一列最大数0.380最接近第一列中第二行的数0.366,因此,第一行乘以得到表3.8左边部分的比值:设机器A生产第1种零件的时间为x,则生产第Ⅱ种零件的时间为1一x;设机器B生产第Ⅱ种零件的时间为y,则生产第Ⅲ种零件的时间为1一y。由成套要求得:105x=56(1一x)+66y=83(1一y)+53整理得:解得:得到表3.8中第二次近似表。三台机器共加工出约70套产品。
相似问题
下列三个∮函数是否符合合格化条件? 请帮忙给出正确答案和分析 谢谢!
下列三个∮函数是否符合合格化条件? 请帮忙给出正确答案和分析,谢谢!
使目标函数y=5x1+6x2达到最大。请帮忙给出正确答案和分析 谢谢!
使目标函数y=5x1+6x2达到最大。请帮忙给出正确答案和分析,谢谢!
某厂有A B C三台机器及三项作业I Ⅱ Ⅲ 要求每台机器只完成一项作业 每项作业只由一台机器完成
某厂有A,B,C三台机器及三项作业I,Ⅱ,Ⅲ,要求每台机器只完成一项作业,每项作业只由一台机器完成,三台机器完成各项作业的费用由表6.9给出。 问
用表上作业法 求解下列(表4.41~表4.43)产销平衡问题的最优调用方案和最小的总运费。 (1)
用表上作业法,求解下列(表4.41~表4.43)产销平衡问题的最优调用方案和最小的总运费。 (1) (2) (3)请帮忙给出正确答案和分析,谢谢!
表2.5是某地区1990至1998年的存款额(单位:亿元): 分别用简单平均法 三项简单移动平均法预
表2.5是某地区1990至1998年的存款额(单位:亿元): 分别用简单平均法、三项简单移动平均法预测1999年的存款额。请帮忙给出正确答案和分析,谢谢!












