微分方程xyy=x2+y2满足y｜x=e=2e的特解为( )．A．y2=2x2(lnx+1)B．y2
微分方程xyy=x2+y2满足y｜x=e=2e的特解为( )．
A．y2=2x2(lnx+1)
B．y2=2x2(In｜x｜+1)
C．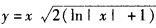
D．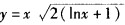
请帮忙给出正确答案和分析，谢谢！
参考解答
456***102
2024-11-16 12:11:35
正确答案：B
微分方程xyy'=x2+y2两边同除以xy可得，则y=ux,将其代入上述微分方程中并化简可得，,即有C．再将代入可得，因为y｜x=e=2e，代人后得到，C=1，此时特解为即为y2=2x2(In｜x｜+1)．故正确答案为B．
相似问题
将10g葡萄糖和甘油分别溶于100g水中 问所得溶液的凝固点各为多少?请帮忙给出正确答案和分析 谢谢
将10g葡萄糖和甘油分别溶于100g水中，问所得溶液的凝固点各为多少?请帮忙给出正确答案和分析，谢谢！
设有无穷级数其α中为常数 则此级数( )．A．绝对收敛B．条件收敛C．发散D．敛散性与α有关请帮忙给
设有无穷级数其α中为常数，则此级数( )．A．绝对收敛B．条件收敛C．发散D．敛散性与α有关请帮忙给出正确答案和分析，谢谢！
设由椭圆柱面z=z2＋2y2与抛物柱而z=2一x2所围立体的体积为_____．由椭圆柱面z=z2+2
设由椭圆柱面z=z2＋2y2与抛物柱而z=2一x2所围立体的体积为_____．由椭圆柱面z=z2+2y2与抛物柱而z=2一x2所围立体的体积为_____．请帮忙给出正确答案和分析，谢谢！
求下列微分方程的通解或在给定条件下的特解： (1)xyˊ＋y＝x3y6； (2)ydx＝－(x＋x2
求下列微分方程的通解或在给定条件下的特解： (1)xyˊ＋y＝x3y6； (2)ydx＝－(x＋x2y2)dy，y(1)＝1．请帮忙给出正确答案和分析，谢谢！
设若y=x(1＋sinx)cosx 则y=_____．若y=x(1+sinx)cosx 则y=___
设若y=x(1＋sinx)cosx，则y=_____．若y=x(1+sinx)cosx，则y=_____．请帮忙给出正确答案和分析，谢谢！
