根据二重积分性质 比较 ∫∫Dln(x+y)d0与∫∫[ln(x+y)]2d0的大小 高等数学复旦
根据二重积分性质,比较 ∫∫Dln(x+y)d0与∫∫[ln(x+y)]2d0的大小
高等数学复旦大学出版第三版下册课后习题答案习题十
根据二重积分性质,比较![]() 的大小,其中:
的大小,其中:
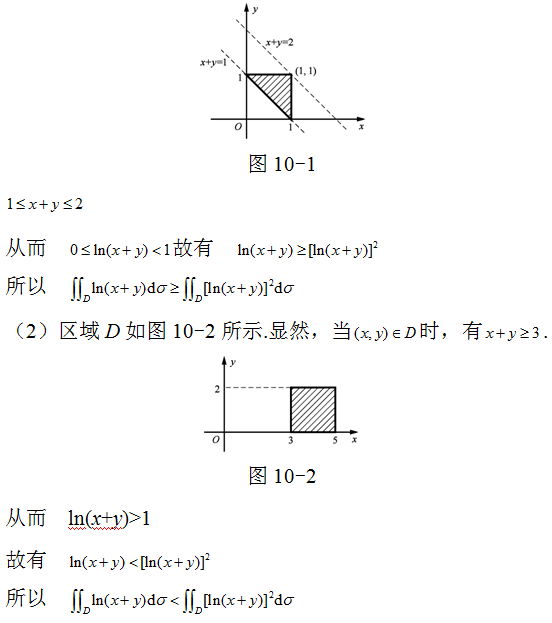
(1)D表示以(0,1),(1,0),(1,1)为顶点的三角形;
(2)D表示矩形区域 .![]()
参考解答
解:(1)区域D如图10-1所示,由于区域D夹在直线x+y=1与x+y=2之间,显然有
答案仅供参考,不要直接抄袭哦
相似问题
试问a为何值时 函数f(x)=a sin x+1/3 sin 3x在x=π/3处取得极值?它是极大值
试问a为何值时,函数f(x)=a sin x+1/3 sin 3x在x=π/3处取得极值?它是极大值还是极小值?并求此极值 试问a为何值时,函数处取得极值?它是极大值
曲线弧y=sin x (0
曲线弧y=sin x (0
设lim(x→1) (x^2+mx+n)/(x-1)=5 求常数m n 的值.设 求常数m n
设lim(x→1) (x^2+mx+n)/(x-1)=5 ,求常数m,n 的值 设 ,求常数m,n 的值
在极坐标系下计算二重积分:(1)∫∫Dsin√x^2+y^2dxdy 高等数学复旦大学出版第三版下
在极坐标系下计算二重积分:(1)∫∫Dsin√x^2+y^2dxdy 高等数学复旦大学出版第三版下册课后习题答案习题十 在极坐标系下计算二重积分:
作适当坐标变换 计算下列二重积分:(1)∫∫Dx2y2dxdy 其中D是由xy=2 xy=4
作适当坐标变换,计算下列二重积分:(1)∫∫Dx2y2dxdy ,其中D是由xy=2, xy=4, x=y, y=3x在第一象限所围平面区域; 高等数学复旦大学出版第三版下册












