在寡头垄断市场上的两个企业 它们的长期成本函数分别为 LTC1=+2Q1 LTC2=+2Q2 面对的
在寡头垄断市场上的两个企业,它们的长期成本函数分别为 LTC1=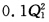 +2Q1 LTC2=
+2Q1 LTC2=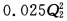 +2Q2 面对的市场需求函数为 P=50-0.1Q 如果这两个企业按古诺模型决策,在实现均衡时,市场价格是什么?各自的产量是多少?各有多大利润? 如果结成卡特尔,实现均衡时,市场价格又是什么?各自的产量又是多少?各有多大利润?这样的卡特尔能够实现吗?怎样才能实现卡特尔?
+2Q2 面对的市场需求函数为 P=50-0.1Q 如果这两个企业按古诺模型决策,在实现均衡时,市场价格是什么?各自的产量是多少?各有多大利润? 如果结成卡特尔,实现均衡时,市场价格又是什么?各自的产量又是多少?各有多大利润?这样的卡特尔能够实现吗?怎样才能实现卡特尔?
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:按古诺模型: MC1=0.2Q1+2 MC2=0.05Q2+2 50-0.2Q1-0.1Q2=0.2Q1+2 50-0.1Q1-0.2Q2=0.05Q2+2 Q1=80Q2=160 P=26 π1=1280 π2=3200 结成卡特尔像一个完全垄断企业那样为总利润最大化两个企业的边际成本横坐标相加得到总边际成本: MC=0.04Q+2 而 MR=50-0.2Q 进而得到 Q1=40Q2=160 P=30 π1=960π2=3840 虽然总利润增加了320但由于企业1的利润减少这样的卡特尔不能形成除非卡特尔规定企业2承诺给企业1转移不少于320的利润如转移480。
按古诺模型:MC1=0.2Q1+2MC2=0.05Q2+250-0.2Q1-0.1Q2=0.2Q1+250-0.1Q1-0.2Q2=0.05Q2+2Q1=80,Q2=160P=26π1=1280,π2=3200结成卡特尔,像一个完全垄断企业那样,为总利润最大化,两个企业的边际成本横坐标相加,得到总边际成本:MC=0.04Q+2而MR=50-0.2Q进而得到Q1=40,Q2=160P=30π1=960,π2=3840虽然总利润增加了320,但由于企业1的利润减少,这样的卡特尔不能形成,除非卡特尔规定企业2承诺给企业1转移不少于320的利润,如转移480。
相似问题
某垄断竞争市场上的一个企业 其生产的总成本函数为 TC=25Q-0.05Q2+0.00005Q3 面
某垄断竞争市场上的一个企业,其生产的总成本函数为 TC=25Q-0.05Q2+0.00005Q3 面对的客观需求函数为 P=30-0.02Q 而企业的决策者认为其面对的
垄断企业实行两部收费是指_______。A.先收入门费 让消费者获得消费资格 再按消费数量收费B.先
垄断企业实行两部收费是指_______。A.先收入门费,让消费者获得消费资格,再按消费数量收费B.先收定金,作为预售;再收全款,完成交易C.先收首付款,
通常电影院首轮上演的贺岁片定价为80元 三个月后降到40元 这是_______。A.一级差别定价B.
通常电影院首轮上演的贺岁片定价为80元,三个月后降到40元,这是_______。A.一级差别定价B.二级差别定价C.两部收费制D.捆绑定价E.以上各项均不对请
变动比例联产品投入要素总量通常是由_______。A.投入要素生产不同联产品的边际生产收益的横坐标相
变动比例联产品投入要素总量通常是由_______。A.投入要素生产不同联产品的边际生产收益的横坐标相加,得到的总边际生产收益曲线和投入要素的边际支出曲
一买方垄断企业面对数量众多的供给者。买方的需求函数为 P=300-0.1Qd 而供给者们的总供给函数
一买方垄断企业面对数量众多的供给者。买方的需求函数为 P=300-0.1Qd 而供给者们的总供给函数为 P=120+0.05Qs 买方为实现利润最大化,应当采购












