解氢原子及类氢离子的s态方程。请帮忙给出正确答案和分析 谢谢！

正确答案：s态只是r的函数记为∮＝∮(r)对照式(2-1-5)s态l＝0其方程为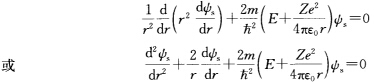 对基态1s方程解的形式为 ∮_1s(r)＝ce^-ar 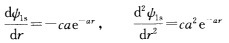代人方程并用ce^-ar除得到 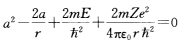上式中1、3项是常数项2、4项是r^-1项。要使得上式恒等于0则常数项和r^-1项分别等于0即 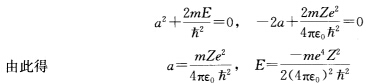式中除Z以外全是常数令 a₀＝4πε₀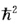／me²＝52．9pm R＝me⁴／2(4πε₀)²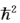＝13．6eV 则a＝Z／a₀E＝Z²R 将a值代人∮_1s(r)＝ce^-ar得∮(r)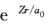＝ 式中系数c值通过归一化确定 ∫∮_1s²dτ＝c²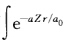dτ＝1 dτ＝r²sinθdθrd∮ 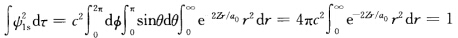利用积分公式∫₀^∞χⁿe^-βχdχ＝n!／(β) 得∫∮_1s²dτ＝4πc².a₀²／4Z³＝1即 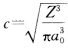得到方程的解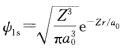
s态只是r的函数,记为∮＝∮(r),对照式(2-1-5),s态l＝0,其方程为对基态1s,方程解的形式为∮1s(r)＝ce-ar代人方程,并用ce-ar除得到上式中1、3项是常数项,2、4项是r-1项。要使得上式恒等于0,则常数项和r-1项分别等于0,即式中除Z以外全是常数,令a0＝4πε0／me2＝52．9pm,R＝me4／2(4πε0)2＝13．6eV则a＝Z／a0,E＝Z2R将a值代人∮1s(r)＝ce-ar得∮(r)＝式中系数c值通过归一化确定∫∮1s2dτ＝c2dτ＝1dτ＝r2sinθdθrd∮利用积分公式∫0∞χne-βχdχ＝n!／(β)得∫∮1s2dτ＝4πc2.a02／4Z3＝1,即得到方程的解